
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是边
是边![]() 上一动点(不与点
上一动点(不与点![]() 重合),以
重合),以![]() 为边在
为边在![]() 的下方作等边三角形
的下方作等边三角形![]() ,连接
,连接![]() .
.
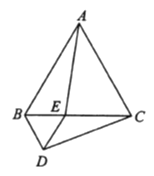
(1)在运动的过程中, ![]() 与
与![]() 有何数量关系?请说明理由.
有何数量关系?请说明理由.
(2)当![]() 时,求
时,求![]() 的度数.
的度数.
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,
, ![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,给出四个结论:①
,给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论有 ( )
;其中正确的结论有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校班际篮球联赛中,每场比赛都要分出胜负,每队胜一场得3分,负一场得1分,如果某班要在第一轮的28场比赛中至少得43分,那么这个班至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
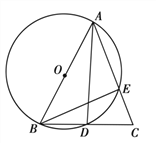
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB·CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cm,若动点
=3 cm,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒1 cm,设出发的时间为
的路径运动,且速度为每秒1 cm,设出发的时间为![]() s.
s.
(1)求出发2s后, ![]() 的面积.
的面积.
(2) ![]() 为何值时,
为何值时, ![]() 为等腰三角形?
为等腰三角形?
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒2 cm,若
的路径运动,且速度为每秒2 cm,若![]() 两点同时出发,当
两点同时出发,当![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分?
的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈用2万元为小明存了一个6年期的教育储蓄,6年后,共能得23456元,则这种教育储蓄的年利率为( )
A.2.86%
B.2.88%
C.2.84%
D.2.82%
查看答案和解析>>
科目:初中数学 来源: 题型:
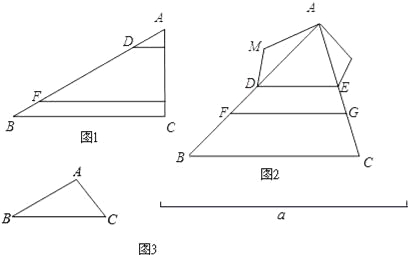
【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , ![]() = .
= .
(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com