
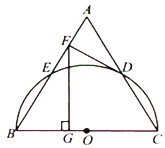
ЎѕМвДїЎїИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬ ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cmЈ¬Иф¶Їµг
=3 cmЈ¬Иф¶Їµг![]() ґУµг
ґУµг![]() їЄКјЈ¬°ґ
їЄКјЈ¬°ґ![]() µДВ·ѕ¶ФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл1 cmЈ¬Йиіц·ўµДК±јдОЄ
µДВ·ѕ¶ФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл1 cmЈ¬Йиіц·ўµДК±јдОЄ![]() s.
s.
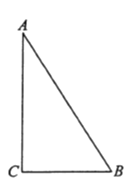
(1)Зуіц·ў2sєуЈ¬ ![]() µДГж»э.
µДГж»э.
(2) ![]() ОЄєОЦµК±Ј¬
ОЄєОЦµК±Ј¬ ![]() ОЄµИСьИэЅЗРО?
ОЄµИСьИэЅЗРО?
(3)БнУРТ»µг![]() Ј¬ґУµг
Ј¬ґУµг![]() їЄКјЈ¬°ґ
їЄКјЈ¬°ґ![]() µДВ·ѕ¶ФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл2 cmЈ¬Иф
µДВ·ѕ¶ФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл2 cmЈ¬Иф![]() БЅµгН¬К±іц·ўЈ¬µ±
БЅµгН¬К±іц·ўЈ¬µ±![]() ЦРУРТ»µгµЅґпЦХµгК±Ј¬БнТ»µгТІНЈЦ№ФЛ¶Ї.µ±
ЦРУРТ»µгµЅґпЦХµгК±Ј¬БнТ»µгТІНЈЦ№ФЛ¶Ї.µ±![]() ОЄєОЦµК±Ј¬Ц±ПЯ
ОЄєОЦµК±Ј¬Ц±ПЯ![]() °С
°С![]() µДЦЬі¤·ЦіЙПаµИµДБЅІї·Ц?
µДЦЬі¤·ЦіЙПаµИµДБЅІї·Ц?
Ўѕґр°ёЎї(1) ![]() µДГж»эОЄ
µДГж»эОЄ![]() cm2;(2) t=3s»т6s»т5.4s»т6.5sЈ¬
cm2;(2) t=3s»т6s»т5.4s»т6.5sЈ¬ ![]() ОЄµИСьИэЅЗРО;(3)µ±
ОЄµИСьИэЅЗРО;(3)µ±![]() ОЄ
ОЄ![]() s»т
s»т![]() sК±Ј¬Ц±ПЯ
sК±Ј¬Ц±ПЯ![]() °С
°С![]() µДЦЬі¤·ЦіЙПаµИµДБЅІї·Ц.
µДЦЬі¤·ЦіЙПаµИµДБЅІї·Ц.
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©АыУГ№ґ№Й¶ЁАнµГіцAC=4cmЈ¬Ѕш¶ш±нКѕіцAPµДі¤Ј¬Ѕш¶шµГіцґр°ёЈ»
ЈЁ2Ј©·ЦБЅЦЦЗйїцЈєўЩИфPФЪ±ЯACЙПК±Ј¬BC=CP=6cmЈ¬ґЛК±УГµДК±јдОЄ6sЈ»ўЪИфPФЪAB±ЯЙПК±Ј¬УРИэЦЦїЙДЬЈєiИфК№BP=CB=6cmЈ¬ґЛК±AP=4cmЈ¬PФЛ¶ЇµДВ·іМОЄ4+8=12cmЈ¬УГµДК±јдОЄ12К±Ј»iiЈ©ИфCP=BC=6cmЈ¬№эCЧчCDЎНABУЪµгDЈ¬ёщѕЭГж»э·ЁЗуµГёЯCD=4.8cmЈ¬ЗуіцBP=2PD=7.2cmЈ¬µГіцPФЛ¶ЇµДВ·іМОЄ18-7.2=10.8cmЈ¬јґїЙµГіцЅб№ыЈ»ўЈЈ©ИфBP=CPЈ¬ФтЎПPCB=ЎПBЈ¬Ц¤іцPA=PCµГіцPA=PB=5cmЈ¬µГіцPµДВ·іМОЄ13cmЈ¬јґїЙµГіцЅб№ыЈ»
ЈЁ3Ј©·ЦБЅЦЦЗйїцЈєўЩµ±PЎўQГ»ПаУцЗ°ЈєPµгЧЯ№эµДВ·іМОЄtЈ¬QЧЯ№эµДВ·іМОЄ2tЈ¬ёщѕЭМвТвµГіц·ЅіМЈ¬Ѕв·ЅіМјґїЙЈ»ўЪµ±PЎўQГ»ПаУцєуЈєµ±PµгФЪABЙПЈ¬QФЪACЙПЈ¬ФтAP=t-8Ј¬AQ=2t-16Ј¬ёщѕЭМвТвµГіц·ЅіМЈ¬Ѕв·ЅіМјґїЙЈ»јґїЙµГіцЅб№ыЈ®
(1)ИзНјўЩЈ¬ТтОЄ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cm
=3 cm
ЛщТФ![]() cm
cm
¶Їµг![]() ґУµг
ґУµг![]() їЄКјЈ¬°ґ
їЄКјЈ¬°ґ![]() µДВ·ѕ¶ФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл1 cmЈ¬ЛщТФіц·ў2sєуЈ¬
µДВ·ѕ¶ФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл1 cmЈ¬ЛщТФіц·ў2sєуЈ¬ ![]() .
.
ТтОЄ![]()
ЛщТФ![]() µДГж»эОЄ
µДГж»эОЄ![]() cm2.
cm2.
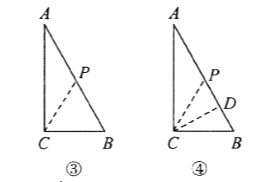
(2)ўЩИзНјўЪЈ¬µ±µг![]() ФЪ±Я
ФЪ±Я![]() ЙПК±Ј¬
ЙПК±Ј¬ ![]() cmЈ¬ґЛК±
cmЈ¬ґЛК±![]() Ј¬
Ј¬ ![]() ОЄµИСьИэЅЗРО;
ОЄµИСьИэЅЗРО;
ўЪµ±µг![]() ФЪ
ФЪ![]() ±ЯЙПК±Ј¬УРИэЦЦЗйїц:
±ЯЙПК±Ј¬УРИэЦЦЗйїц:
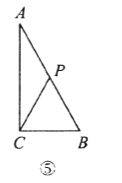
ўс)ИзНјўЫЈ¬Иф![]() cmЈ¬ґЛК±
cmЈ¬ґЛК±![]() cmЈ¬µг
cmЈ¬µг![]() ФЛ¶ЇµДВ·іМОЄ
ФЛ¶ЇµДВ·іМОЄ![]() (cm)Ј¬ґЛК±
(cm)Ј¬ґЛК±![]() Ј¬
Ј¬ ![]() ОЄµИСьИэЅЗРО;
ОЄµИСьИэЅЗРО;
ўт)ИзНјўЬЈ¬Иф![]() cmЈ¬№эµг
cmЈ¬№эµг![]() ЧчР±±Я
ЧчР±±Я![]() µДёЯЅ»
µДёЯЅ»![]() УЪµг
УЪµг![]() Ј¬ёщѕЭГж»э·ЁЗуµГёЯОЄ
Ј¬ёщѕЭГж»э·ЁЗуµГёЯОЄ![]() cmЈ¬ЛщТФ
cmЈ¬ЛщТФ![]() cmЈ¬ЛщТФ
cmЈ¬ЛщТФ![]() cmЈ¬ЛщТФµг
cmЈ¬ЛщТФµг![]() ФЛ¶ЇµДВ·іМОЄ
ФЛ¶ЇµДВ·іМОЄ![]() (cm)Ј¬ґЛК±
(cm)Ј¬ґЛК±![]() Ј¬
Ј¬ ![]() ОЄµИСьИэЅЗРО
ОЄµИСьИэЅЗРО
ўу)ИзНјўЭЈ¬Иф![]() Ј¬ґЛК±
Ј¬ґЛК±![]() У¦ёГОЄР±±Я
У¦ёГОЄР±±Я![]() µДЦРµгЈ¬µг
µДЦРµгЈ¬µг![]() ФЛ¶ЇµДВ·іМОЄ
ФЛ¶ЇµДВ·іМОЄ![]() (cm)Ј¬ґЛК±ЛщУГµДК±јдОЄ
(cm)Ј¬ґЛК±ЛщУГµДК±јдОЄ![]() sЈ¬
sЈ¬ ![]() ОЄµИСьИэЅЗРО.
ОЄµИСьИэЅЗРО.
(3)ИзНјўЮЈ¬µ±µг![]() ФЪ
ФЪ![]() ЙПЈ¬µг
ЙПЈ¬µг![]() ФЪ
ФЪ![]() ЙПК±Ј¬Фт
ЙПК±Ј¬Фт![]() Ј¬
Ј¬ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() s;
s;
ИзНјўЯЈ¬µ±µг![]() ФЪ
ФЪ![]() ЙПЈ¬µг
ЙПЈ¬µг![]() ФЪ
ФЪ![]() ЙПК±Ј¬Фт
ЙПК±Ј¬Фт![]() Ј¬
Ј¬ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() sЈ¬ЛщТФµ±
sЈ¬ЛщТФµ±![]() ОЄ
ОЄ![]() »т
»т![]() К±Ј¬Ц±ПЯ
К±Ј¬Ц±ПЯ![]() °С
°С![]() µДЦЬі¤·ЦіЙПаµИµДБЅІї·Ц.
µДЦЬі¤·ЦіЙПаµИµДБЅІї·Ц.




 И«ДЬІвїШЖЪД©РЎЧґФЄПµБРґр°ё
И«ДЬІвїШЖЪД©РЎЧґФЄПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄµЅЦ±ПЯlµДѕаАлµИУЪaµДЛщУРµгµДјЇєПКЗУлЦ±ПЯlЖЅРРЗТѕаАлОЄaµДБЅМхЦ±ПЯl1Ўўl2ЈЁИзНјўЩЈ©Ј®
ЈЁ1Ј©ФЪНјўЪµДЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬»іцµЅЦ±ПЯy=xЈ«2![]() µДѕаАлОЄ1µДЛщУРµгµДјЇєПµДНјРОЈ®ІўРґіцёГНјРОУлyЦбЅ»µгµДЧш±кЈ®
µДѕаАлОЄ1µДЛщУРµгµДјЇєПµДНјРОЈ®ІўРґіцёГНјРОУлyЦбЅ»µгµДЧш±кЈ®
ЈЁ2Ј©КФМЅМЦФЪТФЧш±кФµгOОЄФІРДЈ¬rОЄ°лѕ¶µДФІЙПЈ¬µЅЦ±ПЯy= x Ј« 2![]() µДѕаАлОЄ1µДµгµДёцКэУлrµД№ШПµЈ®
µДѕаАлОЄ1µДµгµДёцКэУлrµД№ШПµЈ®
ЈЁ3Ј©ИзНјўЫЈ¬ИфТФЧш±кФµгOОЄФІРДЈ¬2ОЄ°лѕ¶µДФІЙПЦ»УРБЅёцµгµЅЦ±ПЯy= x Ј« bµДѕаАлОЄ1Ј¬ФтbµДИЎЦµ·¶О§ОЄ Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬НшёсЦРµДГїёцРЎХэ·ЅРОµД±Яі¤¶јКЗ1Ј¬ГїёцРЎХэ·ЅРОµД¶ҐµгЅРЧцёсµгЈ®
ЎчACBєНЎчDCEµД¶Ґµг¶јФЪёсµгЙПЈ¬EDµДСУі¤ПЯЅ»ABУЪµгFЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЎчACBЎЧЎчDCEЈ»ЈЁ2Ј©ЗуЦ¤ЈєEFЎНABЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬µИ±ЯИэЅЗРО![]() µД±Яі¤ОЄ4Ј¬µг
µД±Яі¤ОЄ4Ј¬µг![]() КЗ±Я
КЗ±Я![]() ЙПТ»¶Їµг(І»Улµг
ЙПТ»¶Їµг(І»Улµг![]() ЦШєП)Ј¬ТФ
ЦШєП)Ј¬ТФ![]() ОЄ±ЯФЪ
ОЄ±ЯФЪ![]() µДПВ·ЅЧчµИ±ЯИэЅЗРО
µДПВ·ЅЧчµИ±ЯИэЅЗРО![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() .
.
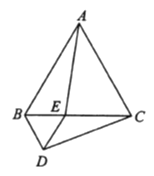
(1)ФЪФЛ¶ЇµД№эіМЦРЈ¬ ![]() Ул
Ул![]() УРєОКэБї№ШПµ?ЗлЛµГчАнУЙ.
УРєОКэБї№ШПµ?ЗлЛµГчАнУЙ.
(2)µ±![]() К±Ј¬Зу
К±Ј¬Зу![]() µД¶ИКэ.
µД¶ИКэ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИфТ»ёцБЅО»КэёцО»КэЧЦОЄaЈ¬К®О»КэЧЦ±ИёцО»КэЧЦ¶а1Ј¬ФтХвБЅёцКэОЄЈЁ Ј©
A.a+1
B.a+10
C.10a+1
D.11a+10
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТФµИ±ЯИэЅЗРОABCµДBC±ЯОЄЦ±ѕ¶»°лФІЈ¬·Ц±рЅ»ABЎўACУЪµгEЎўDЈ¬DFКЗФІµДЗРПЯЈ¬№эµгFЧчBCµДґ№ПЯЅ»BCУЪµгGЈ®ИфAFµДі¤ОЄ2Ј¬ФтFGµДі¤ОЄ
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ADЎўBCКЗЎСOµДБЅМх»ҐПаґ№Ц±µДЦ±ѕ¶Ј¬µгPґУµгOіц·ўЈ¬СШOЎъCЎъDЎъOµДВ·ПЯФИЛЩФЛ¶ЇЈ¬ЙиЎПAPB=yЈЁµҐО»Јє¶ИЈ©Ј¬ДЗГґyУлµгPФЛ¶ЇµДК±јдxЈЁµҐО»ЈєГлЈ©µД№ШПµНјКЗ ( )
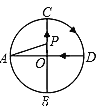
A. 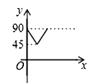 B.
B. 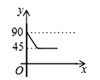 C.
C. 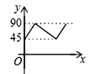 D.
D. 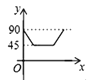
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїБР·ЅіМ»т·ЅіМЧйЅвУ¦УГМвЈє
ОЄБЛПмУ¦КРХюё®Ў°ВМЙ«іцРРЎ±µДєЕХЩЈ¬РЎХЕЙППВ°аУЙЧФјЭіµ·ЅКЅёДОЄЖпЧФРРіµ·ЅКЅЈ®ТСЦЄРЎХЕµҐО»УлЛыјТПаѕа20З§ГЧЈ¬ЙППВ°аёЯ·еК±¶ОЈ¬ЧФјЭіµµДЖЅѕщЛЩ¶ИКЗЧФРРЖЅѕщіµЛЩ¶ИµД2±¶Ј¬ЖпЧФРРіµЛщУГК±јд±ИЧФјЭіµЛщУГК±јд¶а![]() РЎК±Ј®ЗуЧФјЭіµЖЅѕщЛЩ¶ИєНЧФРРіµЖЅѕщЛЩ¶ИёчКЗ¶аЙЩЈї
РЎК±Ј®ЗуЧФјЭіµЖЅѕщЛЩ¶ИєНЧФРРіµЖЅѕщЛЩ¶ИёчКЗ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com