
【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
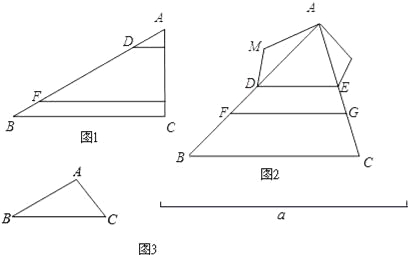
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , ![]() = .
= .
(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
【答案】(1)3、2;(2)证明见解析;(3)作图见解析.
【解析】试题分析:解决本题要用到了平行线分线段成比例、相似三角形的判定与性质、平行线的判定.
(1) 两条直线被一组平行线所截,所得的对应线段成比例;
(2)要证∠M=∠N,只需证△AMD∽△ANE,只需证![]() ,由于DF=DM,EG=EN,BF=AM,GC=AN,只需证
,由于DF=DM,EG=EN,BF=AM,GC=AN,只需证![]() ,根据“两条直线被一组平行线所截,所得的对应线段成比例”即可解决问题;
,根据“两条直线被一组平行线所截,所得的对应线段成比例”即可解决问题;
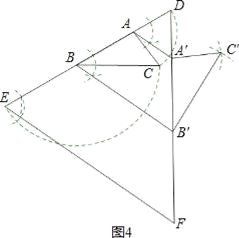
(3)借鉴图2,可进行以下操作:①延长BA到D,使得AD=AC,延长AB到E,使得BE=BC;②过点D画一条线段DF,使得DF=a,连接EF;③过点B作∠DBB′=∠DEF,交DF于点B′,过点A作∠DAA′=∠DEF,交DF于点A′,即可得到AA′∥BB′∥EF;④以点A′为圆心,A′D为半径画弧,以点B′为圆心,B′F为半径画弧,两弧交于点C′;⑤连接A′C′,B′C′,如图4,△A′B′C′即为所求作.
解:(1)如图1,
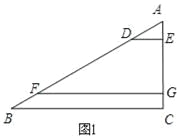
∵DE∥FG∥BC,
∴![]() ,
,
∴![]() .
.
∵AD=2,AE=1,DF=6,
∴![]() ,
,
∴EG=3, ![]() =2.
=2.
故答案分别为:3、2;
(2)如图2,
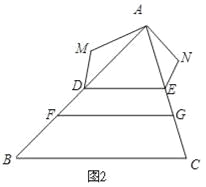
∵DE∥FG∥BC,
∴![]() ,
,
∴![]() .
.
∵DF=DM,EG=EN,BF=AM,GC=AN,
∴![]() ,
,
∴△AMD∽△ANE,
∴∠M=∠N;
(3)步骤:
①延长BA到D,使得AD=AC,延长AB到E,使得BE=BC;
②过点D画一条线段DF,使得DF=a,连接EF;
③过点B作∠DBB′=∠DEF,交DF于点B′,过点A作∠DAA′=∠DEF,交DF于点A′;
④以点A′为圆心,A′D为半径画弧,以点B′为圆心,B′F为半径画弧,两弧交于点C′;
⑤连接A′C′,B′C′,如图4,△A′B′C′即为所求作.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是边
是边![]() 上一动点(不与点
上一动点(不与点![]() 重合),以
重合),以![]() 为边在
为边在![]() 的下方作等边三角形
的下方作等边三角形![]() ,连接
,连接![]() .
.
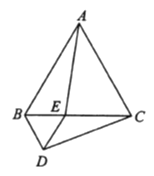
(1)在运动的过程中, ![]() 与
与![]() 有何数量关系?请说明理由.
有何数量关系?请说明理由.
(2)当![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应市政府“绿色出行”的号召,小张上下班由自驾车方式改为骑自行车方式.已知小张单位与他家相距20千米,上下班高峰时段,自驾车的平均速度是自行平均车速度的2倍,骑自行车所用时间比自驾车所用时间多![]() 小时.求自驾车平均速度和自行车平均速度各是多少?
小时.求自驾车平均速度和自行车平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.

请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x≠1,(1+x)(1-x)=1-![]() ,(1-x)(1+x+
,(1-x)(1+x+![]() )=1-
)=1-![]() ,(1-x)(1+x+
,(1-x)(1+x+![]() +
+![]() )=1-
)=1-![]() .
.
(1)根据以上式子计算:
①(1-2)×(1+2+![]() +
+![]() +
+![]() +
+![]() ):②2+
):②2+![]() +
+![]() +…+
+…+![]() (n为正整数):
(n为正整数):
③(x-1)( ![]() +
+![]() +
+![]() +…+
+…+![]() +x+1).
+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=______________:②(a-b) (![]() +ab+
+ab+![]() )=_________________:
)=_________________:
③(a-b)( ![]() +
+![]() b+
b+![]() +
+![]() )=_____________.
)=_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com