
分析 (1)总费用除以单价即为数量,设乙种图书的单价为x元,则甲种图书的单价为1.5x元,根据两种图书数量之间的关系列方程;
(2)设购进甲种图书a本,则购进乙种图书(40-a)本,①根据总费用等于购买的甲种图书的费用+购买的甲种图书的费用即可求得函数关系式;②根据“投入的经费不超过1050元,甲种图书数量不少于乙种图书的数量”列出不等式组解决问题.
(3)根据题意得$\left\{\begin{array}{l}{30a+20b=690①}\\{a+b>30②}\end{array}\right.$,由①得a=$\frac{69-2b}{3}$=23-$\frac{2}{3}$b,代入②解得b>21,因为a、b都是整数,即可求得b的取值.
解答 解:(1)设乙种图书的单价为x元,则甲种图书的单价为1.5x元,由题意得$\frac{600}{x}$-$\frac{600}{1.5x}$=10
解得:x=20
则1.5x=30,
经检验得出:x=20是原方程的根,
答:甲种图书的单价为30元,乙种图书的单价为20元;
(2)①设购进甲种图书a本,则购进乙种图书(40-a)本,根据题意得:
W=30a+20(40-a)=800+10a,
即W=10a+800;
②$\left\{\begin{array}{l}{10a+800≤1050}\\{a≥40-a}\end{array}\right.$
解得:20≤a≤25,
所以a=20、21、22、23、24、25,则40-a=20、19、18、17、16、15
∴共有6种方案;
由W=10a+800可知:
当a取最小值时,W最小,
∴a=20,W最小=1000元;
(3)根据题意得$\left\{\begin{array}{l}{30a+20b=690①}\\{a+b>30②}\end{array}\right.$,
由①得a=$\frac{69-2b}{3}$=23-$\frac{2}{3}$b,
代入②解得b>21,
∵a、b都是整数,
∴b必须是3的倍数,
∴b=24,27,30,33.
故答案为24,27.
点评 此题考查一次函数的应用,分式方程的运用,一元一次不等式组的运用,理解题意,抓住题目蕴含的数量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
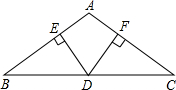 在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.
在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
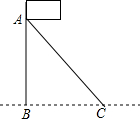 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )| A. | 6sin50° | B. | 6cos50° | C. | $\frac{6}{sin50°}$ | D. | $\frac{6}{cos50°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
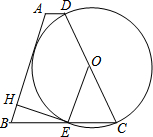 如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.
如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com