
【题目】已知:如图,等边三角形ABD与等边三角形ACE具有公共顶点A,连接CD,BE,交于点P.
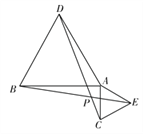
(1)观察度量, ![]() 的度数为____.(直接写出结果)
的度数为____.(直接写出结果)
(2)若绕点A将△ACE旋转,使得![]() ,请你画出变化后的图形.(示意图)
,请你画出变化后的图形.(示意图)
(3)在(2)的条件下,求出![]() 的度数.
的度数.
【答案】(1)120°;(2)作图见解析;(3)∠BPC =120°.
【解析】分析:(1)∠BPC的度数为120°,理由为:由△ABD与△ACE都是等边三角形,利用等边三角形的性质得到∠DAB=∠ABD=∠CAE=60°,AD=AB,AC=AE,利用等式的性质得到夹角相等,利用SAS得出三角形DAC与三角形BAE全等,由全等三角形的对应角相等得到∠ADC=∠ABE,利用外角性质,等量代换即可得到所求;(2)作出相应的图形,如图所示;(3)解法同(1),求出∠BPC的度数即可.
本题解析:
(1)∠BPC的度数为120°,理由为:
 证明:∵△ABD与△ACE都是等边三角形,
证明:∵△ABD与△ACE都是等边三角形,
∴∠DAB=∠ABD=∠CAE=60°,AD=AB,AC=AE,
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
在△DAC与△BAE中,
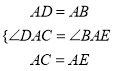 ,∴△DAC≌△BAE(SAS),
,∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,∵∠ADC+∠CDB=60°,∴∠ABE+∠CDB=60°,
∴∠BPC=∠DBP+∠PDB=∠ABE+∠CDB+∠ABC=120°;
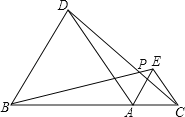
(2)作出相应的图形,如图所示;
(3)∵△ABD与△ACE都是等边三角形,
∴∠ADB=∠BAD=∠ABD=∠CAE=60°,AD=AB,AC=AE,
∴∠DAB+∠DAE=∠CAE+∠DAE,即∠DAC=∠BAE,
在△DAC与△BAE中,
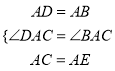 ,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ABE+∠DBP=60°,
,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ABE+∠DBP=60°,
∴∠ADC+∠DBP=60°,∴∠BPC=∠BDP+∠PBD=∠ADC+∠DBP+∠ADB=120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于![]() cm2?
cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:①上海明天是晴天,②铅球浮在水面上,③平面中,多边形的外角和都等于360度,属于确定事件的个数有( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有20位同学参加乒乓球、羽毛球比赛,甲说:“只参加一项的人数大于14人。”乙说:“两项都参加的人数小于5人。”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A. 若甲对,则乙对 B. 若乙对,则甲对
C. 若乙错,则甲错 D. 若甲错,则乙对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com