
【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
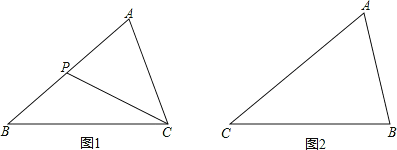
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)王华补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.
【答案】∠ACP=∠B(或∠APC=∠ACB),或AC2=APAB;(1)∠ACP=∠B(或∠APC=∠ACB);或AC2=APAB;理由见解析;(2)50°.
【解析】
试题分析:(1)由∠A=∠A,当∠ACP=∠B,或∠APC=∠ACB;或![]() 时,△ACP∽△ABC;
时,△ACP∽△ABC;
(2)延长AB到点D,使BD=BC,连接CD,由已知条件得出证出![]() ,由∠A=∠A,证出△ACB∽△ADC,得出对应角相等∠ACB=∠D,再由等腰三角形的性质和三角形内角和定理得出∠ACB+∠BCD+∠D+∠A=180°,得出∠ACB=50°即可.
,由∠A=∠A,证出△ACB∽△ADC,得出对应角相等∠ACB=∠D,再由等腰三角形的性质和三角形内角和定理得出∠ACB+∠BCD+∠D+∠A=180°,得出∠ACB=50°即可.
试题解析:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或![]() ,即AC2=APAB时,△ACP∽△ABC;
,即AC2=APAB时,△ACP∽△ABC;
(1)王华补充的条件是:∠ACP=∠B(或∠APC=∠ACB);或AC2=APAB;理由如下:
∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或![]() ,即AC2=APAB时,△ACP∽△ABC;
,即AC2=APAB时,△ACP∽△ABC;
(2)延长AB到点D,使BD=BC,连接CD,如图所示:
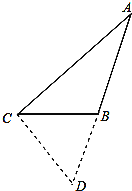
∵AC2=AB2+ABBC=AB(AB+BC)=AB(AB+BD)=ABAD,
∴![]() ,
,
又∵∠A=∠A,∴△ACB∽△ADC,
∴∠ACB=∠D,
∵BC=BD,
∴∠BCD=∠D,
在△ACD中,∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.


科目:初中数学 来源: 题型:
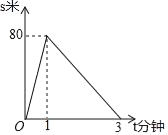
【题目】大课间到了,小明和小欢两人打算从教室匀速跑到600米外的操场做课间操,刚出发时小明就发现鞋带松了,停下来系鞋带,小欢则直接前往操场,小明系好鞋带后立即沿同一路开始追赶小欢,小明在途中追上小欢后继续前行,小明到达操场时课间操还没有开始,于是小明站在操场等待,小欢继续前往操场,设小明和小欢两人想距s(米),小欢行走的时间为t(分钟),s关于t的函数的部分图象如图所示,当两人第三次相距60米时,小明离操场还有_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),……直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1、l2、l3、…、ln分别交于点A1、A2、A3、…、An;函数y=2x的图象与直线l1、l2、l3、…、ln分别交于点B1、B2、B3、…、Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2018=( )
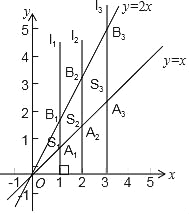
A. 2017.5B. 2018C. 2018.5D. 2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 过点
过点![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,作
,作![]() 轴于点
轴于点![]() .设点
.设点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() .
.
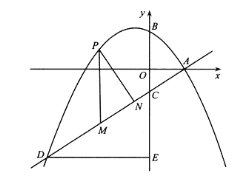
(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)探究:是否存在这样的点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)设![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“加倍”矩形.
的“加倍”矩形.
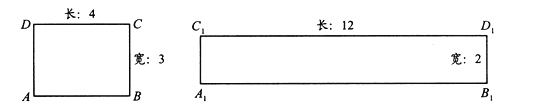
解决问题:
(1)当矩形的长和宽分别为3,2时,它是否存在“加倍”矩形?若存在,求出“加倍”矩形的长与宽,若不存在,请说明理由.
(2)边长为![]() 的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
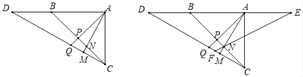
【题目】如图,△ABC中,∠BAC=90°,∠ABC=45°,点D为AB延长线上一点,连接CD,∠AMC=90°,AM交BC于点N,∠APB=90°,AP交CD于点Q.
(1)求证:AN=CQ;
(2)如图,点E在BA的延长线上,且AD=BE,连接EN并延长交CD于点F,求证:DQ=EN;
(3)在(2)的条件下,当3AE=2AB时,请直接写出EN:FN的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
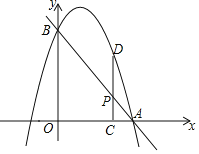
【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )
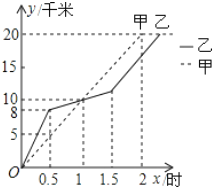
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com