
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 过点
过点![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,作
,作![]() 轴于点
轴于点![]() .设点
.设点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() .
.
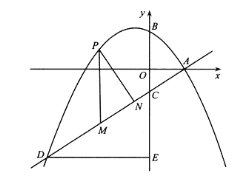
(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)探究:是否存在这样的点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)设![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)存在,点
;(2)存在,点![]() 的坐标是
的坐标是![]() 和
和![]() ;(3)
;(3)![]() ,
,![]() 的最大值是15.
的最大值是15.
【解析】
(1)将A,B两点分别代入y=![]() x2+bx+c求出b,c,将A代入y=kx-
x2+bx+c求出b,c,将A代入y=kx-![]() 求出k;
求出k;
(2)首先假设出P,M点的坐标,进而得出PM的长,将两函数联立得出D点坐标,进而得出CE的长,利用平行四边形的判定得出PM=CE时四边形PMEC是平行四边形,得出等式方程求解并判断即可;
(3)利用勾股定理得出DC的长,进而根据△PMN∽△DCE,得出两三角形周长之比,求出l与x的函数关系,再利用配方法求出二次函数最值即可.
解:(1):(1)把A(2,0),B(0,![]() )代入y=
)代入y=![]() x2+bx+c得
x2+bx+c得 ,
,
解得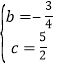 ;
;
把A(2,0)代入y=kx-![]() 得2k-
得2k-![]() =0,解得k=
=0,解得k=![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
(2)设![]() 的坐标是
的坐标是![]() ,则
,则![]() 的坐标是
的坐标是![]() ,
,
∴![]()
![]() ,
,
解方程 ,得:
,得: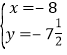 ,
,![]() ,
,
∵点![]() 在第三象限,则点
在第三象限,则点![]() 的坐标是
的坐标是![]() ,
,
由![]() 得点
得点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,
由于![]() 轴,所以当
轴,所以当![]() 时四边形
时四边形![]() 是平行四边形.
是平行四边形.
即![]() ,
,
解这个方程得:![]() ,
,![]() ,符合
,符合![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
综上所述:点![]() 的坐标是
的坐标是![]() 和
和![]() ;
;
(3)在![]() 中,
中,![]() ,
,![]()
由勾股定理得:![]()
∴![]() 的周长是24,
的周长是24,
∵![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,即
,即![]()
化简整理得:![]() 与
与![]() 的函数关系式是:
的函数关系式是:![]() ,
,
![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 的最大值是15.
的最大值是15.


科目:初中数学 来源: 题型:
【题目】解决问题:
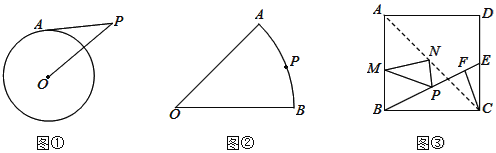
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
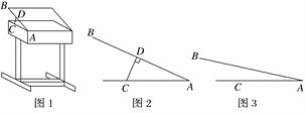
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 经过正方形网格中的格点
经过正方形网格中的格点![]() 、
、![]() 、
、![]() 、
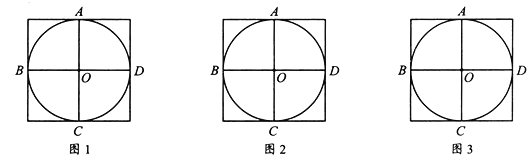
、![]() ,请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的
,请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的![]() :
:
(1)顶点![]() 在
在![]() 上且不与点
上且不与点![]() 、
、![]() 、
、![]() 、
、![]() 重合;
重合;
(2)![]() 在图1、图2、图3中的正切值分别为1、
在图1、图2、图3中的正切值分别为1、![]() 、2.
、2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
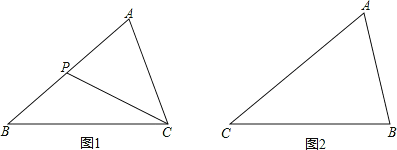
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)王华补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
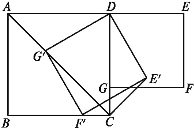
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:
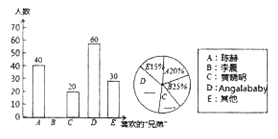
(1)本次被调查的学生有_______人.
(2)将两幅统计图补充完整.
(3)若从3名喜欢“李晨”的学生和2名喜欢“![]() ”的学生中随机抽取两人参加文体活动,用树状图或列表法求出两人都是喜欢“李晨”的学生的概率.
”的学生中随机抽取两人参加文体活动,用树状图或列表法求出两人都是喜欢“李晨”的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com