
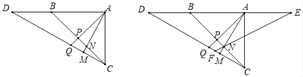
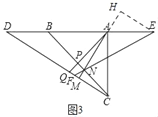
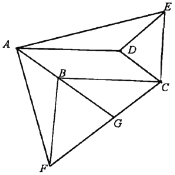
【题目】如图,△ABC中,∠BAC=90°,∠ABC=45°,点D为AB延长线上一点,连接CD,∠AMC=90°,AM交BC于点N,∠APB=90°,AP交CD于点Q.
(1)求证:AN=CQ;
(2)如图,点E在BA的延长线上,且AD=BE,连接EN并延长交CD于点F,求证:DQ=EN;
(3)在(2)的条件下,当3AE=2AB时,请直接写出EN:FN的值为 .
【答案】(1)证明见解析;(2)证明见解析;(3)25:3.
【解析】
(1)利用ASA证明△APN≌△CPQ,可得AN=CQ;
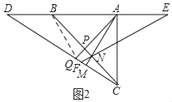
(2)如图2,连接BQ,证明△DBQ≌△EAN(SAS),可得DQ=EN;
(3)设AE=2x,AB=3x,则BD=2x,DC=![]() x,作辅助线,构建直角三角形和相似三角形,证明△AHE∽△AMD和△DQA∽△ANC,得
x,作辅助线,构建直角三角形和相似三角形,证明△AHE∽△AMD和△DQA∽△ANC,得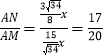 ,设AH=8m,AM=20m,AN=17m,再证明△EHN∽△FMN,可得结论.
,设AH=8m,AM=20m,AN=17m,再证明△EHN∽△FMN,可得结论.
解:(1)证明:∵∠APB=90°
∴∠APN=∠CPQ=90°,
∴∠PNA+∠NAP=∠NAP+∠CQP=90°,
∴∠PNA=∠CQP,
∵AB=AC,∠BAC=90°,
∴AP=PC,
∴△APN≌△CPQ(ASA),
∴AN=CQ;
(2)证明:如图2,连接BQ,
由(1)知:AP是BC的垂直平分线,
∴BQ=CQ,
∵AN=CQ,
∴AN=BQ,
∵BQ=CQ,
∴∠QBC=∠QCB=∠NAP,
∵∠PBA=∠PAB=45°,
∴∠QBA=∠BAN,
∴∠DBQ=∠NAE,
∵BD=AE,
∴△DBQ≌△EAN(SAS),
∴DQ=EN;
(3)∵3AE=2AB,
∴设AE=2x,AB=3x,则BD=2x,DC=![]() x,
x,
如图3,过E作EH⊥AM,交MA的延长线于H,
∴∠H=∠AMD=90°,
∴EH∥DC,
∴∠HEA=∠CDA,
∴△AHE∽△AMD,
∴![]() ,
,
∵∠MAC=∠CDA,∠ACN=∠DAQ=45°,
∴△DQA∽△ANC,
∴![]() ,
,
由(2)知:CQ=AN,
∴![]() ,
,
∴AN=CQ=![]() ,
,
S△ADC=![]() ,
,
![]() ,
,
AM=![]() ,
,
∴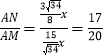 ,
,
∴设AH=8m,AM=20m,AN=17m,
则MN=3m,
∵EH∥FM,
∴△EHN∽△FMN,
∴![]() .
.
故答案为:25:3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
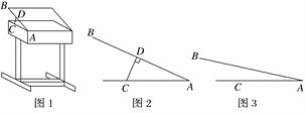
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
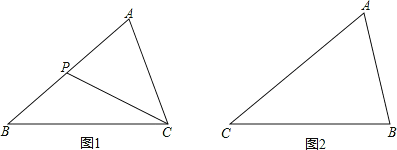
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)王华补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在半圆O上,半径OB=2![]() ,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )

A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
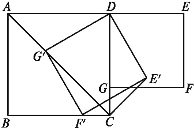
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
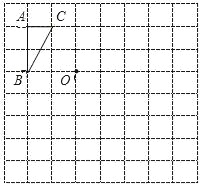
【题目】如图8×8正方形网格中,点A、B、C和O都为格点.
(1)利用位似作图的方法,以点O为位似中心,可将格点三角形ABC扩大为原来的2倍.请你在网格中完成以上的作图(点A、B、C的对应点分别用A′、B′、C′表示);
(2)当以点O为原点建立平面坐标系后,点C的坐标为(﹣1,2),则A′、B′、C′三点的坐标分别为:A′: B′: C′: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广安市红色旅游资源丰富,无论是小平故里行,还是华蓥山上游,都吸引了不少游客。2014~2018年旅游收入不断增长,同比增速分别为:17.3%,14.7%,17.3%,16.5%,19.1%,关于这组数据,下列说法正确的是( ).
A. 中位数是14.7%B. 众数是17.3%
C. 平均数是17.98%D. 方差是0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com