计算:(-14)15×230= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

计算：（-

）¹⁵×2³⁰=

．

考点：幂的乘方与积的乘方

专题：

分析：根据幂的乘方，可化成指数相同的幂的乘法，根据积的乘方，可得答案．

解答：解；原式=（-

）¹⁵×4¹⁵=[（-

）×4]¹⁵=-1，
故答案为：-1．

点评：本题考查了幂的乘方与积的乘方，利用法则计算是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

我们在七年级下册第五章学习过：能够完全重合的两个图形成为全等形．事实上，对于两个二次函数的图象如果能够完全重合，我们就称这两个二次函数的图象为全等抛物线．经研究可知：对于任意两个二次函数：y₁=a₁x²+b₁x+c₁和y₂=a₂x²+b₂x+c₂（a₁≠0，a₂≠0），当|a₁|=|a₂|时，这两个二次函数的图象就为全等抛物线．
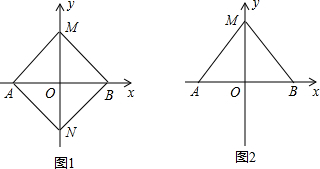
现有△ABM，A（-1，0），B（1，0）．记过三点的二次函数抛物线为“C_□□□”（“□□□”中填写相应三个点的字母）
（1）若已知M（0，1），N（0，-1），且△ABM≌△ABN．请通过计算判断C_ABM与C_ABN是否为全等抛物线；
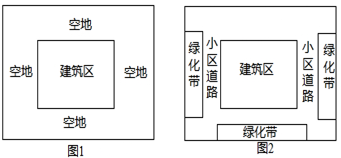
（2）在图2中，以A、B、M三点为顶点，画出平行四边形．若已知M（0，n），求抛物线C_ABM的解析式，并直接写出所有过平行四边形中三个顶点且能与C_ABM全等的抛物线解析式．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图1，某小区的平面图是一个占地长500米，宽400米的矩形，正中央的建筑区是与整个小区长宽比例相同的矩形，如果要使四周的空地所占面积是小区面积的19%，南北空地等宽，东西空地等宽．
（1）求该小区四周的空地的宽度；
（2）如图2，该小区在东、西、南三块空地上做如图所示的矩形绿化带，绿化带与建筑区之间为小区道路，小区道路宽度一致．已知东、西两侧绿化带完全相同，其长均为200米，南侧绿化带的长为300米，绿化面积为5500平方米，请算出小区道路的宽度．