
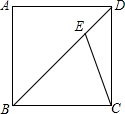
 如图,正方形ABCD中,E为BD上一点,∠DCE=22.5°
如图,正方形ABCD中,E为BD上一点,∠DCE=22.5°分析 (1)利用正方形的对角线平分每组对角,再利用等腰三角形的判定方法得出即可;
(2)利用(1)中所求,再结合勾股定理得出即可.
解答 (1)证明:∵四边形ABCD是正方形,BD为对角线,
∴∠BDC=∠CBE=45°,
∵∠DCE=22.5°,
∴∠BCE=67.5°,
∴∠BEC=180°-45°-67.5°=67.5°,
∴∠BCE=∠BEC,
∴BE=BC;
(2)解:设BC=DC=a,
则BC=$\sqrt{2}$a,
∵BE=BC,
∴$\frac{DE}{BE}$=$\frac{DE}{BC}$=$\frac{BD-BC}{BC}$=$\frac{\sqrt{2}a-a}{a}$=$\sqrt{2}$-1.
点评 此题主要考查了等腰三角形的判断以及正方形的性质,得出∠CBD=45°是解题关键.


科目:初中数学 来源: 题型:填空题
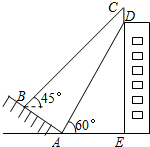 如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为5.4米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为5.4米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com