
分析 分析情况,得弦AB、CD可能在圆心的同侧或两侧,利用垂径定理构造直角三角形即可以求出答案.
解答 解:做已知圆垂直于弦AB、CD的直径,交AB于点E,交CD于点F,
连接OB、OD,
∵OE⊥AB,OF⊥CD,弦AB=6,弦CD=8,
∴BE=3,CF=4,
(1)当弦AB、CD在圆心同侧时,如下图:
OE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
OF=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴EF=4-3=1.
(2)当弦AB、CD在圆心两侧时,如下图: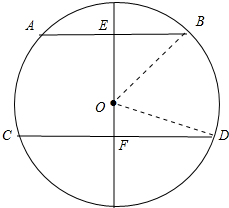
OE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
OF=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴EF=4+3=7.
故答案为:1或7.
点评 题目考查了垂径定理的应用和勾股定理,题目设计很好,学生需要注意不要出现漏解现象.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
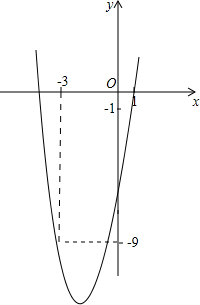 如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).
如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com