
| A. | $\frac{{a}^{2014}-1}{a-1}$ | B. | $\frac{{a}^{2014}-1}{a}$ | C. | $\frac{{a}^{2015}-1}{a-1}$ | D. | $\frac{{a}^{2015}-1}{a}$ |
分析 设S=1+a+a2+a3+a4+…+a2014①,在①式的两边同时都乘以a得:aS=a+a2+a3+a4+…+a2014+a2015②,两式相减即可得出答案.
解答 解:设S=1+a+a2+a3+a4+…+a2014①,
在①式的两边同时都乘以a得:aS=a+a2+a3+a4+…+a2014+a2015②,
②-①得:(a-1)S=a2015-1,
S=$\frac{{a}^{2015}-1}{a-1}$,
即1+a+a2+a3+a4+…+a2014=$\frac{{a}^{2015}-1}{a-1}$,
故选C.
点评 本题考查了整式的混合运算和求值的应用,能读懂题意是解此题的关键,用了类比思想.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:初中数学 来源: 题型:填空题
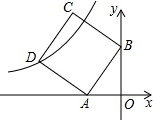 在平面直角坐标系中,正方形ABCD如图摆放,点A的坐标为(-1,0),点B的坐标为(0,2),点D在反比例函数y=$\frac{k}{x}$(k<0)图象上,将正方形沿x轴正方向平移m个单位长度后,点C恰好落在该函数图象上,则m的值是1.
在平面直角坐标系中,正方形ABCD如图摆放,点A的坐标为(-1,0),点B的坐标为(0,2),点D在反比例函数y=$\frac{k}{x}$(k<0)图象上,将正方形沿x轴正方向平移m个单位长度后,点C恰好落在该函数图象上,则m的值是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
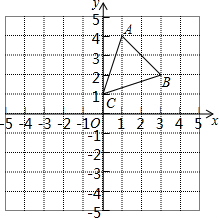 如图,三角形ABC是原三角形A1B1C1经过先向右平移3个单位长度,再向上平移1个单位长度得到的.请画出原三角形A1B1C1,并写出点A1、B1、C1的坐标.
如图,三角形ABC是原三角形A1B1C1经过先向右平移3个单位长度,再向上平移1个单位长度得到的.请画出原三角形A1B1C1,并写出点A1、B1、C1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则a-c<b-c | B. | 若a>b,则-a+c>-b+c | ||
| C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
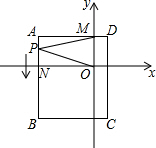 如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(-4,2)、(1,-4),且AD∥x轴,交y轴于M点,AB交x轴于N.
如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(-4,2)、(1,-4),且AD∥x轴,交y轴于M点,AB交x轴于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2=21 | B. | $\frac{1}{2}$x(x-1)=21 | C. | $\frac{1}{2}$x2=21 | D. | x(x-1)=21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com