
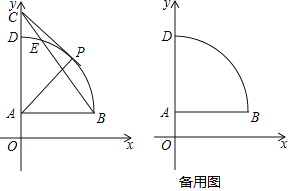
【题目】如图,A(0,2),B(6,2),C(0,c)(c>0),以A为圆心AB长为半径的![]() 交y轴正半轴于点D,
交y轴正半轴于点D,![]() 与BC有交点时,交点为E,P为
与BC有交点时,交点为E,P为![]() 上一点.
上一点.
(1)若c=6![]() +2,
+2,
①BC= ,![]() 的长为 ;
的长为 ;
②当CP=6![]() 时,判断CP与⊙A的位置关系,井加以证明;
时,判断CP与⊙A的位置关系,井加以证明;
(2)若c=10,求点P与BC距离的最大值;
(3)分别直接写出当c=1,c=6,c=9,c=11时,点P与BC的最大距离(结果无需化简)
【答案】(1)①12,π;②详见解析;(2)①![]() ;②
;②![]() (3)答案见详解
(3)答案见详解
【解析】
(1)①先求出AB,AC,进而求出BC和∠ABC,最后用弧长公式即可得出结论;②判断出△APC是直角三角形,即可得出结论;
(2)分两种情况,利用三角形的面积或锐角三角函数即可得出结论;
(3)画图图形,同(2)的方法即可得出结论.
(1)①如图1,
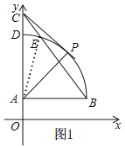
∵c=6![]() +2,
+2,
∴OC=6![]() +2,
+2,
∴AC=6![]() +2﹣2=6
+2﹣2=6![]() ,
,
∵AB=6,
在Rt△BAC中,根据勾股定理得,BC=12,tan∠ABC=![]() =
=![]() ,
,
∴∠ABC=60°,
∵AE=AB,
∴△ABE是等边三角形,
∴∠BAE=60°,
∴∠DAE=30°,
∴![]() 的长为
的长为![]() =π,
=π,
故答案为:12,π;
②CP与⊙A相切.
证明:∵AP=AB=6,AC=OC﹣OA=6![]() ,
,
∴AP2+CP2=108,
又AC2=(6![]() )2=108,
)2=108,
∴AP2+PC2=AC2.
∴∠APC=90°,即:CP⊥AP.
而AP是半径,
∴CP与⊙A相切.
(2)若c=10,即AC=10﹣2=8,则BC=10.
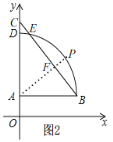
①若点P在![]() 上,AP⊥BE时,点P与BC的距离最大,设垂足为F,
上,AP⊥BE时,点P与BC的距离最大,设垂足为F,
则PF的长就是最大距离,如图2,
S△ABC=![]() AB×AC=
AB×AC=![]() BC×AF,
BC×AF,
∴AF=![]() =
=![]() ,
,
∴PF=AP﹣AF=![]() ;
;
②如图3,若点P在![]() 上,作PG⊥BC于点G,
上,作PG⊥BC于点G,
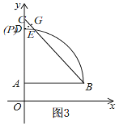
当点P与点D重合时,PG最大.
此时,sin∠ACB=![]() ,
,
即PG=![]() =
=![]()
∴若c=10,点P与BC距离的最大值是![]() ;
;
(3)当c=1时,如图4,
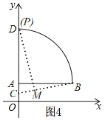
过点P作PM⊥BC,sin∠BCP=![]()
∴PM=![]() =
=![]() ;
;
当c=6时,如图5,同c=10的①情况,PF=6﹣![]() =
=![]() ,
,
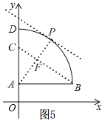
当c=9时,如图6,同c=10的①情况,PF=![]() ,
,
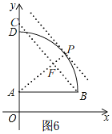
当c=11时,如图7,
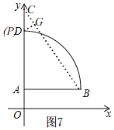
点P和点D重合时,点P到BC的距离最大,同c=10时②情况,DG=![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
查看答案和解析>>
科目:初中数学 来源: 题型:
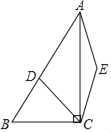
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=4,D是AB上一个动点,将点D绕点C顺时针旋转60°,得到点E,连接AE.若AE=![]() ,则BD=_____.
,则BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
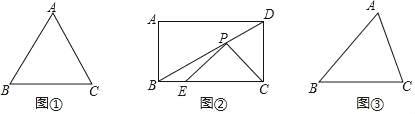
(1)如图①,已知等边△ABC,边长为4,则△ABC的外接圆的半径长为 .
(2)如图②,在矩形ABCD中,AB=4,对角线BD与边BC的夹角为30°,点E在为边BC上且BE=![]() BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
问题解决:
(3)为了迎接新年的到来,西安城墙举办了迎新年大型灯光秀表演.其中一个镭射灯距城墙30米,镭射灯发出的两根彩色光线夹角为60°,如图③,若将两根光线(AB,AC)和光线与城墙的两交点的连接的线段(BC)看作一个三角形,记为△ABC,那么该三角形周长有没有最小值?若有,求出最小值,若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
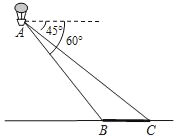
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,![]() ≈1.72).
≈1.72).
查看答案和解析>>
科目:初中数学 来源: 题型:
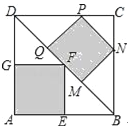
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .
的值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边分别交CB、
绕点A顺时针旋转,它的两边分别交CB、![]() 或它们的延长线
或它们的延长线![]() 于点M、N,当
于点M、N,当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,则
,则

![]() 线段BM、DN和MN之间的数量关系是______;
线段BM、DN和MN之间的数量关系是______;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 如图
如图![]() 的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
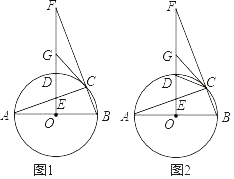
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com