
【题目】如图①,在![]() 中,已知
中,已知![]() 分别是
分别是![]() 上的两点,且
上的两点,且![]() .
.![]() .
.
![]() 求梯形
求梯形![]() 的面积;
的面积;
![]() 如图②,有一梯形
如图②,有一梯形![]() 与梯形
与梯形![]() 重合,固定
重合,固定![]() ,将梯形
,将梯形![]() 向右运动,当点D与点C重合时梯形
向右运动,当点D与点C重合时梯形![]() 停止运动;
停止运动;

①若某时段运动后形成的四边形![]() 中,
中,![]() 求运动路程
求运动路程![]() 的长,并求此时
的长,并求此时![]() 的值;
的值;
②设运动中![]() 的长度为
的长度为![]() ,试用含
,试用含![]() 的代数式表示梯形
的代数式表示梯形![]() 与
与![]() 重合部分面积
重合部分面积![]() .
.
【答案】(1)梯形![]() 的面积为16;(2)①BD=4,G′B2
的面积为16;(2)①BD=4,G′B2![]() ;②当0≤x<
;②当0≤x<![]() 时,S=
时,S=![]() ;当
;当![]() ≤x≤
≤x≤![]() 时,S=
时,S=![]() .
.
【解析】
(1)在Rt△ABC中由AB=AC得到∠ABC=∠ACB=45°,又由GF∥BC得到∠AGF=∠AFG=45°,由此得到AG=AF=2,AB=AC=6,然后根据S梯形BCFG=S△ABCS△AGF进行计算;
(2)①根据平移可知BDG′G是平行四边形,又DG⊥BG′,所以BDG′G是菱形,由此得到BD=BG=4,如图③,过点G′作G′M⊥BC于点M,在Rt△G′DM中,求出DM=G'M=![]() ,接着得到BM=
,接着得到BM=![]() ,然后在Rt△G′BM中,根据勾股定理可以求出G'B2;②在Rt△AGF与Rt△ABC中分别求出GF,BC,当0≤x<
,然后在Rt△G′BM中,根据勾股定理可以求出G'B2;②在Rt△AGF与Rt△ABC中分别求出GF,BC,当0≤x<![]() 时,其重合部分为梯形,如图②,过G点作GH垂直BC于点H,得GH=
时,其重合部分为梯形,如图②,过G点作GH垂直BC于点H,得GH=![]() ,而BD=GG′=x,DC=
,而BD=GG′=x,DC=![]() ,G'F'=
,G'F'=![]() ,根据梯形面积公式即可用x表示S;当
,根据梯形面积公式即可用x表示S;当![]() ≤x≤
≤x≤![]() 时,其重合部分为等腰直角三角形,如图③,斜边DC=
时,其重合部分为等腰直角三角形,如图③,斜边DC=![]() ,斜边上的高为
,斜边上的高为![]() ,根据三角形面积公式即可用x表示S.
,根据三角形面积公式即可用x表示S.
解:(1)∵在Rt△ABC中,AB=AC,
∴∠ABC=∠ACB=45°,
∵GF∥BC,
∴∠AGF=∠AFG=45°,
∴AG=AF=2,AB=AC=6,
∴S梯形BCFG=S△ABCS△AGF=![]() ×6×6
×6×6![]() ×2×2=16;
×2×2=16;
(2)①∵在运动过程中有DG′∥BG且DG′=BG,
∴BDG′G是平行四边形,
当DG⊥BG′时,BDG′G是菱形,
∴BD=BG=4,
如图③,当BDG′G为菱形时,过点G′作G′M⊥BC于点M,
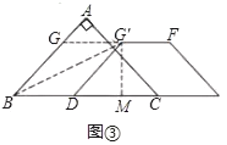
在Rt△G′DM中,∠G′DM=45°,DG′=4,
∴DM=G′M且DM2+G'M2=DG'2,
∴DM=G′M=![]() ,
,
∴BM=![]() ,
,
连接G′B.
在Rt△G′BM中,G′B2=BM2+G′M2=![]() ;
;
②在Rt△AGF与Rt△ABC中,GF=![]() ,BC=
,BC=![]() ,
,
当0≤x<![]() 时,其重合部分为梯形,如图②,
时,其重合部分为梯形,如图②,
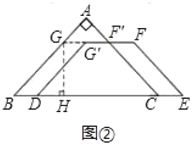
过G点作GH垂直BC于点H,则GH=![]() ,
,
∵BD=GG′=x,
∴DC=![]() ,G′F′=
,G′F′=![]() ,
,
∴S=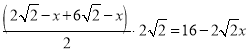 ;
;
当![]() ≤x≤
≤x≤![]() 时,其重合部分为等腰直角三角形,如图③,
时,其重合部分为等腰直角三角形,如图③,

∵斜边DC=![]() ,
,
∴斜边上的高为![]() ,
,
∴S=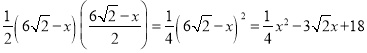 .
.


科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(2,1)=![]()
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求p的取值范围;
恰好有3个整数解,求p的取值范围;
(2)若T(x,y)=T(y,x)对任意有理数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ![]() ②
② ![]() ③
③ ![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ![]() ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当 ![]() 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究“掷一枚图钉,钉尖朝上”的概率,两个小组用同一个图钉做试验进行比较,他们的统计数据如下:
掷图钉的次数 | 50 | 100 | 200 | 300 | 400 |
钉尖朝上 的次数 | |||||
第一小组 | 23 | 39 | 79 | 121 | 160 |
第二小组 | 24 | 41 | 81 | 124 | 164 |
(1)请你估计第一小组和第二小组所得的概率分别是多少?
(2)你认为哪一个小组的结果更准确?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com