
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.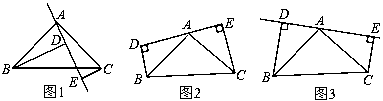
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
【答案】
(1)解:在△ABD和△CAE中,
∵∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAD=∠ABD.
又∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.又AE=AD+DE,∴AE=DE+CE,即BD=DE+CE
(2)解:BD=DE﹣CE.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.又AB=AC,∠ADB=∠CEA=90°,∴△ADB≌△CEA.∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,即 BD=DE﹣CE
(3)解:同理:BD=DE﹣CE
【解析】(1)根据已知条件证明△ABD≌△CAE,可得BD=AE,AD=CE,则结论可得;(2)关系是:BD=DE﹣CE,证明方法同(1);(3)同理:BD=DE﹣CE。


科目:初中数学 来源: 题型:
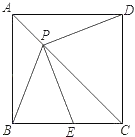
【题目】如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.
(1)求证:①PE=PD;②PE⊥PD;
(2)设AP=x,△PBE的面积为y.
①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7![]() (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( ).
A.3
B.![]()
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,a,b,c分别是ΔABC中∠A,∠B,∠C的对边,P为BC上一点,以AP为直径的圆O交AB于D,PE∥AB交AC于E,b,c是方程x2+kx+9=0的两根,且(b2+c2)(b2+c2-14)-72=0,锐角B的正弦值等于![]() 。
。
(1)求K的值;
(2)设BD=x,求四边形ADPE的面积为S关于x的函数关系式;
(3)问圆O是否能与BC相切?若能请求出x的值;若不能,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com