
【题目】如图,点P是射线BM上的一个动点(点P不与点B重合),∠AOB= 30°,∠ABM=60°.当∠OAP=______时,以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

【答案】75°或120°或90°
【解析】
先根据题意画出符合的情况,再根据等腰三角形的性质和三角形内角和定理求出即可.
分为以下5种情况:
①OA=OP,
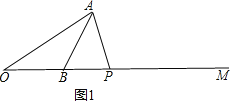
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=![]() ×(180°-30°)=75°;
×(180°-30°)=75°;
②OA=AP,
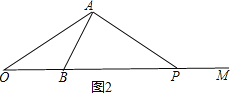
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-30°=120°;
③AB=AP,
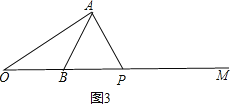
∵∠ABM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°;
④AB=BP,
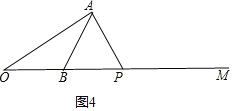
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=![]() ×(180°-60°)=60°,
×(180°-60°)=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°;
⑤AP=BP,
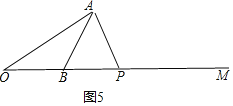
∵∠ABM=60°,AP=BP,
∴∠ABO=∠PAB=60°,
∴∠APO=180°-60°-60°=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°;
所以当∠OAP=75°或120°或90°时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形,
故答案为:75°或120°或90°.


科目:初中数学 来源: 题型:
【题目】小明在解一元二次方程时,发现有这样一种解法:
如:解方程![]() .
.
解:原方程可变形,得: ![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
直接开平方并整理,得. ![]() ,
, ![]() .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程![]() 时写的解题过程.
时写的解题过程.
解:原方程可变形,得: ![]() .
.
![]() ,
,
![]() .
.
直接开平方并整理,得. ![]() ,
, ![]() .
.
上述过程中的a、b、c、d表示的数分别为 , , , .
(2)请用“平均数法”解方程: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
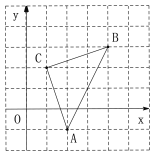
【题目】如图,直角坐标系中,三角形ABC的顶点都在网格点上,其中A(2,![]() ), B(4,3), C(1,2).
), B(4,3), C(1,2).
(1)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形![]() ,则三角形
,则三角形![]() 的三个顶点坐标。
的三个顶点坐标。![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
(2)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=2cm,AE=1cm,求⊙O的半径.
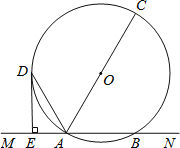
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是大家公认的![]() 商用元年.移动通讯行业人员想了解
商用元年.移动通讯行业人员想了解![]() 手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生![]() 手机的使用情况
手机的使用情况
D.该调査中的样本容量是500位大学生
查看答案和解析>>
科目:初中数学 来源: 题型:
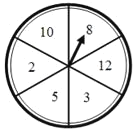
【题目】小亮、小颖的手上都有两根长度分别为5、8的木棒,小亮与小颖都想通过转动转盘游戏来获取第三根木棒,如图,一个均匀的转盘被平均分成6等份,分别标有木棒的长度2,3,5,8,10,12这6个数字.小亮与小颖各转动转盘一次,停止后,指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜,三根木棒能组成等腰三角形则小颖获胜.
(1)小亮获胜的概率是 ;
(2)小颖获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,她连续转动转盘10次,都没转到5和8,能不能就说小颖获胜的可能性为0?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交CD于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值;
的值;
(3)在(2)的条件下,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com