
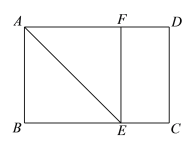
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,过E作EF⊥AD于F.
(1)求证:四边形ABEF是正方形;
(2)连接BF交AE于点O,连接DO,若CD=2,CE=1,求OD的长.
【答案】(1)证明见解析;(2)OD的长为![]() .
.
【解析】
(1)先根据矩形的判定可得出四边形ABEF是矩形,再根据角平分线的性质可得![]() ,然后根据正方形的判定即可得证;
,然后根据正方形的判定即可得证;
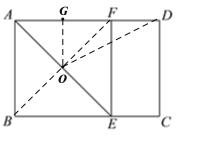
(2)如图(见解析),过点O作![]() 于点G,先根据正方形的性质得出点O为AE的中点,再根据中位线定理可得
于点G,先根据正方形的性质得出点O为AE的中点,再根据中位线定理可得![]() 的长,从而可得DG的长,然后利用勾股定理求解即可.
的长,从而可得DG的长,然后利用勾股定理求解即可.
(1)![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]()
![]()
![]()
![]() 四边形ABEF是矩形
四边形ABEF是矩形
又![]() 平分
平分![]()
![]() (角平分线的性质)
(角平分线的性质)
![]() 矩形ABEF是正方形
矩形ABEF是正方形
即四边形ABEF是正方形;
(2)如图,过点O作![]() 于点G,则
于点G,则![]()
同(1)可得:四边形CDFE是矩形
![]()
由(1)可知,四边形ABEF是正方形
![]() ,点O是对角线AE的中点
,点O是对角线AE的中点
![]()
![]() OG是
OG是![]() 的中位线
的中位线
![]() ,点G是AF的中点
,点G是AF的中点
![]()
![]()
在![]() 中,
中,![]()
故OD的长为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
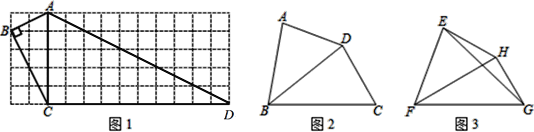
(1)如图1,已知四边形![]() 在正方形网格中,顶点都在格点上,判断:四边形
在正方形网格中,顶点都在格点上,判断:四边形![]() ______(填“是”或“不是”)以
______(填“是”或“不是”)以![]() 为“相似对角线”的四边形;
为“相似对角线”的四边形;
(2)如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() 平分
平分![]() .求证:
.求证:![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
(3)如图![]() ,已知
,已知![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,![]() .连接
.连接![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
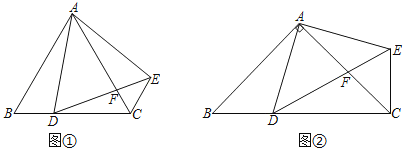
【题目】如图①,在△ABC中,AB=AC,∠BAC=60°,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转60°得到AE,连接EC,则:
(1)①∠ACE的度数是 ; ②线段AC,CD,CE之间的数量关系是 .
(2)如图②,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,请判断线段AC,CD,CE之间的数量关系,并说明理由;
(3)如图②,AC与DE交于点F,在(2)条件下,若AC=8,求AF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数)的对称轴为
为常数)的对称轴为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,![]() 的最大值为5,顶点为
的最大值为5,顶点为![]() ,过点
,过点![]() 且平行于
且平行于![]() 轴的直线与抛物线交于点
轴的直线与抛物线交于点![]() ,
,![]() .
.

(1)求该二次函数的解析式和点![]() ,
,![]() 的坐标.
的坐标.
(2)点![]() 是直线
是直线![]() 上的动点,若点
上的动点,若点![]() ,点
,点![]() ,点
,点![]() 所构成的三角形与
所构成的三角形与![]() 相似,求出所有点
相似,求出所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
 根据表、图提供的信息,解决以下问题:
根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
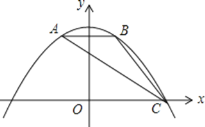
【题目】如图,抛物线![]() 经过
经过![]() 的三个顶点,与
的三个顶点,与![]() 轴相交于
轴相交于![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴,
轴,![]() 轴, 垂足分别为点
轴, 垂足分别为点![]() ,
,![]() ,当四边形
,当四边形![]() 为正方形时,求出点
为正方形时,求出点![]() 的坐标;
的坐标;
(3)将(2) 中的正方形![]() 沿
沿![]() 向右平移,记平移中的正方形
向右平移,记平移中的正方形![]() 为正方形
为正方形![]() ,当点
,当点![]() 和点
和点![]() 重合时停止运动, 设平移的距离为
重合时停止运动, 设平移的距离为![]() ,正方形的边
,正方形的边![]() 与
与![]() 交于点
交于点![]() ,
,![]() 所在的直线与
所在的直线与![]() 交于点
交于点![]() , 连接
, 连接![]() ,是否存在这样的
,是否存在这样的![]() ,使
,使![]() 是等腰三角形?若存在,求
是等腰三角形?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
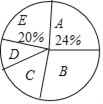
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com