练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，已知等腰直角三角形ABM，∠AMB=90°，C在BM的延长线上，连接AC，并在AM上取点F，使FM=CM．判断BF与AC的关系并说明理由．

    分析 根据全等三角形的判定定理得到△ACM≌△BFM，由全等三角形的性质即可得到结论．

    解答 解：BF=AC，
    理由：在△ACM与△BFM中，
    $\left\{\begin{array}{l}{AM=BM}\\{∠AMC=∠AMB}\\{CM=FM}\end{array}\right.$，
    ∴△ACM≌△BFM，
    ∴BF=AC．

    点评 本题考查了全等三角形的判定和性质，熟练掌握全等三角形的判定和性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

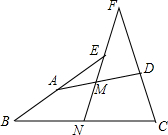    5．在四边形ABCD中，AB=CD，M、N分别是AD和BC的中点，延长BA和CD分别交射线NM于点E和点F，若tan∠F=$\frac{3}{4}$，FC=FN，EN=$\frac{3}{2}$，则EF=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．去括号得：-（a+2b-3c）=-a-2b+3c．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

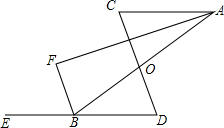    3．请在括号内完成证明过程和填写上推理依据．
    如图，已知：AB和CD相交于点O，∠C=∠AOC，∠D=∠BOD，延长DB到点E，且∠CAB的平分线AF和∠ABE的平分线BF相交于点F．
    求证：AF⊥BF．
    证明：∵∠C=∠AOC，∠D=∠BOD
    又∵∠COA=∠BOD（对顶角相等）
    ∴∠C=∠D∴AC∥BD（内错角相等，两直线平行）
    ∴∠CAB+∠ABE=180°（两直线平行，同旁内角互补）
    ∵∠CAB的平分线AF和∠ABE的平分线BF相交于点F
    ∴∠FAB=$\frac{1}{2}$∠CAB，∠ABF=$\frac{1}{2}$∠ABE
    ∴$\frac{1}{2}∠CAB+\frac{1}{2}∠ABE=\frac{1}{2}×{180°}$
    即∠FAB+∠ABF=90°
    又∵∠FAB+∠ABF+∠AFB=180°
    ∴∠AFB=90°∴AF⊥BF（垂直定义）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，直线y=k（x-2）+k-1与x轴、y轴分别交于B、C两点，且$\frac{OB}{OC}$=$\frac{1}{2}$．
    （1）求B点坐标和k值；
    （2）若点A（x，y）是直线y=k（x-2）+k-1（k＞0）上在第一象限内的一个动点．
    ①当点A在运动过程中，试写出△AOB的面积S与x的函数关系式；（不要求写出自变量的取值范围）
    ②当A点运动到什么位置时，△AOB的面积为$\frac{9}{4}$，并说明理由；
    ③在②成立的情况下，x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出满足条件的所有P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

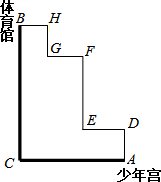    20．如图，粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线．
    ①比较两条线路的长短（简要在下图上画出比较的痕迹）；
    ②小丽坐出租车由体育馆B到少年宫A，假设出租车的收费标准为：起步价为7元，3千米以后每千米1.8元，用代数式表示出租车的收费m元与行驶路程s（s＞3）千米之间的关系；
    ③如果这段路程长4.5千米，小丽身上有10元钱，够不够小丽坐出租车由体育馆到少年宫呢？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF=48°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

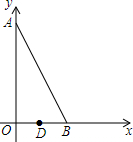    4．如图，在平面直角坐标系xOy中，点A在y轴上，点B在x轴上，∠ABO=60°，若点D（1，0）且BD=2OD．把△ABO绕着点D逆时针旋转m°（0＜m＜180）后，点B恰好落在初始Rt△ABO的边上，此时的点B记为B′，则点B′的坐标为（2，$\sqrt{3}$）或（0，$\sqrt{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．清镇出租车司机小李某天下午运营全是在东西走向的云站路上行驶，如果规定向东为正，向西为负，这天下午他的行车里程（单位：千米）如下：+10，-6，+5，-10，+5，-7，-8，+9，+4，-9，+7
    （1）将最后一名乘客送到目的地时，小李距下午出车时的出发点多远？
    （2）若汽车耗油量为0.12升/千米，这天下午小李共耗油多少升？

    查看答案和解析>>

    同步练习册答案