
 如图,直线y=k(x-2)+k-1与x轴、y轴分别交于B、C两点,且$\frac{OB}{OC}$=$\frac{1}{2}$.
如图,直线y=k(x-2)+k-1与x轴、y轴分别交于B、C两点,且$\frac{OB}{OC}$=$\frac{1}{2}$.分析 (1)首先求得直线y=k(x-2)+k-1与y轴的交点,则OC的长度即可求解,进而求得B的坐标,把B的坐标代入解析式即可求得k的值;
(2)①②根据三角形的面积公式即可求解;
③分O,P,A分别是等腰三角形的顶角顶点三种情况进行讨论,利用等腰三角形的性质即可求解.
解答 解:(1)在y=k(x-2)+k-1中,令x=0,则y=-k-1,
故C的坐标是(0,-k-1),
OC=|-k-1|,令y=0,则x=$\frac{k+1}{k}$,
故B的坐标是($\frac{k+1}{k}$,0),OB=$\frac{k+1}{k}$,
∵$\frac{OB}{OC}$=$\frac{1}{2}$,
∴$\frac{{|{k+1}|}}{k(k+1)}=\frac{1}{2}$
当k+1>0时,$\frac{{|{k+1}|}}{k(k+1)}=\frac{k+1}{k(k+1)}=\frac{1}{k}=\frac{1}{2}$
∴k=2,
把k=2代入B的坐标中,
则B的坐标是:($\frac{3}{2}$,0)
当k+1<0时,$\frac{{|{k+1}|}}{k(k+1)}=\frac{-(k+1)}{k(k+1)}=\frac{-1}{k}=\frac{1}{2}$
∴k=-2,
把k=-2代入B的坐标中,
则B的坐标是:($\frac{1}{2}$,0);
(2)①∵k>0,
∴k=2,
∴OB=$\frac{3}{2}$,
则S=$\frac{1}{2}$×$\frac{3}{2}$(2x-3)=$\frac{3}{2}$x-$\frac{9}{4}$;
②根据题意得:$\frac{3}{2}$x-$\frac{9}{4}$=$\frac{9}{4}$,
解得:x=3,
则A的坐标是(3,3);
?OA=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
当O是△AOP的顶角顶点时,则P的坐标是(-3$\sqrt{2}$,0)或(3$\sqrt{2}$,0);
当A是△AOP的顶角顶点时,则P的坐标是(6,0);
当P是△AOP的顶角顶点时,则P的坐标是(3,0)
点评 本题考查了一次函数与等腰三角形的性质,待定系数法求函数的解析式,正确进行讨论是关键.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等腰直角三角形ABM,∠AMB=90°,C在BM的延长线上,连接AC,并在AM上取点F,使FM=CM.判断BF与AC的关系并说明理由.
如图,已知等腰直角三角形ABM,∠AMB=90°,C在BM的延长线上,连接AC,并在AM上取点F,使FM=CM.判断BF与AC的关系并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
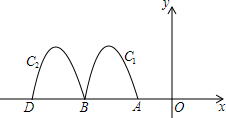 如图,抛物线y=-2x2-8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向左平移得C2,C2与x轴交于点B,D.若直线y=-x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2-8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向左平移得C2,C2与x轴交于点B,D.若直线y=-x+m与C1,C2共有3个不同的交点,则m的取值范围是( )| A. | -3<m<-$\frac{15}{8}$ | B. | $-3<m<-\frac{7}{4}$ | C. | -2<m<$\frac{1}{8}$ | D. | -3<m<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正数 | B. | 奇数 | ||
| C. | 偶数 | D. | 有时为奇数;有时为偶数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com