
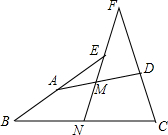
 在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=$\frac{3}{4}$,FC=FN,EN=$\frac{3}{2}$,则EF=1.
在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=$\frac{3}{4}$,FC=FN,EN=$\frac{3}{2}$,则EF=1. 分析 连接BD,点K为BD的中点;连接KM、KN;延长MN至G点,使EG=EB,连接BG,根据三角形中位线定理可得KM∥AB,AB=2KM、KN∥CD,CD=2KN,再证明△EBG和△FCN均为等腰三角形,△EBG≌△FCN可得EG=FN,从而可得EF=NG,过B点作GN的垂线BH交GN于H点.由tan∠F=$\frac{3}{4}$,设BH=3a,进而可得EH=4a、BE=5a,再用含a的代数式表示出EN,再由EN=$\frac{3}{2}$,可得a的值,进而可得答案.
解答  解:连接BD,点K为BD的中点;连接KM、KN;延长MN至G点,使EG=EB,连接BG.
解:连接BD,点K为BD的中点;连接KM、KN;延长MN至G点,使EG=EB,连接BG.
∵M、N分别是AD和BC的中点,
∴KM∥AB,AB=2KM、KN∥CD,CD=2KN.
∵AB=CD,
∴KM=KN,
∴△KMN为等腰三角形,
∴∠KMN=∠KNM,
∵KM∥AB
∴∠BEG=∠KMN,
∵KN∥CD,
∴∠F=∠KNM
∴∠F=∠KNM=∠KMN=∠BEG,
∵FC=FN、EB=EG,
∴△EBG和△FCN均为等腰三角形,且△EBG∽△FCN.
∴∠G=∠C=∠FNC,
又∵∠BNG=∠FNC,
∴∠G=∠BNG,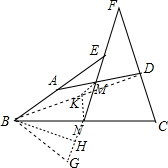
∴△BGN为等腰三角形,
∴BN=BG,∠EBG=∠G,
∴BG=CN,∠EBG=∠FNC,
在△EBG和△FNC中$\left\{\begin{array}{l}{∠G=∠C}\\{BG=CN}\\{∠FNC=∠EBG}\end{array}\right.$,
∴△EBG≌△FCN(ASA),
∴EG=FN,
∴EF=NG,
过B点作GN的垂线BH交GN于H点.
由△BGN为等腰△可知,HN=HG,
∵tan∠F=$\frac{3}{4}$,
∴设BH=3a.
∴tan∠BEG=tan∠F=$\frac{3}{4}$,
∴EH=4a、BE=5a,
∴HG=HN=BE-EH=a,
∵EN=HE-HN=4a-a=3a,
∵EN=$\frac{3}{2}$,所以3a=$\frac{3}{2}$,
∴a=$\frac{1}{2}$,EF=NG=2a=1,
故答案为:1.
点评 此题主要考查了三角形中位线定理,以及全等三角形的判定和性质,等腰三角形的判定和性质,关键是正确作出辅助线,证明出△EBG≌△FCN.


科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{5}{2}$,-$\frac{3}{2}$) | B. | ($\frac{5}{2}$,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,$\frac{5}{2}$) | D. | (-2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).若点D在线段BC上运动,DE交AC于E.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).若点D在线段BC上运动,DE交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等腰直角三角形ABM,∠AMB=90°,C在BM的延长线上,连接AC,并在AM上取点F,使FM=CM.判断BF与AC的关系并说明理由.
如图,已知等腰直角三角形ABM,∠AMB=90°,C在BM的延长线上,连接AC,并在AM上取点F,使FM=CM.判断BF与AC的关系并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com