
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据已知画出图象,把x=-2代入得:4a-2b+c=0,由抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{-2+{x}_{1}}{2}$>$\frac{1}{2}$,即$\frac{b}{a}$<1,由a<0,两边都乘以a得:b>a,对称轴x=-$\frac{b}{2a}$<0,则b<0,得出a<b<0.由一元二次方程根与系数的关系知x1•x2=$\frac{c}{a}$<-2,结合a<0得2a+c>0,;把x=-1代入得到a-b+c>0;根据-$\frac{b}{2a}$<0,推出a<0,b<0,a+c>b,计算2a+c=2b-2a>0;代入得到2a-b+1=-$\frac{1}{2}$c+1>0,根据结论判断即可.
解答 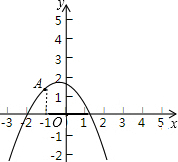 解:根据二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,画出图象为:如图
解:根据二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,画出图象为:如图
把x=-2代入得:4a-2b+c=0,
∴①正确;
由图象开口向下知a<0,
由y=ax2+bx+c与x轴的另一个交点坐标为(x1,0 ),且1<x1<2,
则该抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{-2+{x}_{1}}{2}$>$\frac{1}{2}$,即$\frac{b}{a}$<1,
由a<0,两边都乘以a得:b>a,
∵a<0,对称轴x=-$\frac{b}{2a}$<0,
∴b<0,
∴a<b<0.
∴②正确;
∵(-2,0)、(x1,0),且1<x1,
∴取符合条件1<x1<2的任何一个x1,-2•x1<-2,
∴由一元二次方程根与系数的关系知 x1•x2=$\frac{c}{a}$<-2,
∴不等式的两边都乘以a(a<0)得:c>-2a,
∴2a+c>0,
∴③正确;
④由4a-2b+c=0得 2a-b=-$\frac{c}{2}$,
而0<c<2,∴-1<-$\frac{c}{2}$<0
∴-1<2a-b<0
∴2a-b+1>0,
∴④正确.
所以①②③④三项正确.
故选D.
点评 本题主要考查对二次函数图象上点的坐标特征,抛物线与X轴的交点,二次函数与系数的关系等知识点的理解和掌握,能根据图象确定与系数有关的式子得符号是解此题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | y=3(x-1)2-2 | B. | y=3(x+1)2-2 | C. | y=3(x+1)2+2 | D. | y=3(x-1)2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OA,OB,OC是圆的三条半径.
如图,OA,OB,OC是圆的三条半径.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
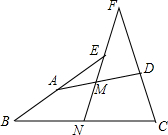 在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=$\frac{3}{4}$,FC=FN,EN=$\frac{3}{2}$,则EF=1.
在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=$\frac{3}{4}$,FC=FN,EN=$\frac{3}{2}$,则EF=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请在括号内完成证明过程和填写上推理依据.
请在括号内完成证明过程和填写上推理依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com