
 如图,OA,OB,OC是圆的三条半径.
如图,OA,OB,OC是圆的三条半径.分析 (1)根据按比例分配,可得扇形的圆心角;
(2)根据按比例分配,可得扇形的面积.
解答 解:(1)∠AOB的度数是360×$\frac{1}{1+2+3}$=60°,
∠AOC的度数是360×$\frac{2}{1+2+3}$=120°,
∠BOC的度数是360×$\frac{3}{1+2+3}$=180°;
(2)这三个扇形的面积分别是:
4π×$\frac{1}{6}$=$\frac{2}{3}$π(cm2),
4π×$\frac{2}{6}$=$\frac{4}{3}$π(cm2),
4π×$\frac{3}{6}$=2π(cm2).
故这三个扇形的面积分别是:$\frac{2}{3}$πcm2,$\frac{4}{3}$πcm2,2πcm2.
点评 本题考查了认识平面图形,利用按比例分配是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
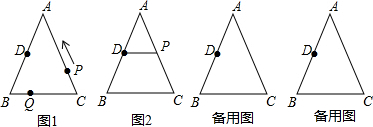
 探究题:
探究题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点A的坐标是(1,2),连接OA,将线段OA绕着点O顺时针旋转,使点A的对应点A′恰好落在x轴正半轴上,则点A′的坐标是($\sqrt{5}$,0).
如图,在平面直角坐标系中,点A的坐标是(1,2),连接OA,将线段OA绕着点O顺时针旋转,使点A的对应点A′恰好落在x轴正半轴上,则点A′的坐标是($\sqrt{5}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.
如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com