
 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.
如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.科目:初中数学 来源: 题型:解答题
 如图,OA,OB,OC是圆的三条半径.
如图,OA,OB,OC是圆的三条半径.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
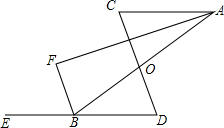 请在括号内完成证明过程和填写上推理依据.
请在括号内完成证明过程和填写上推理依据.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
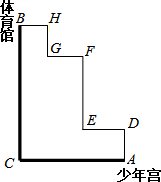 如图,粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
如图,粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com