
分析 (1)根据题意得出是好数,要么是奇数要么能被4整除,进而得出答案;
(2)首先得出从小到大的“好数”为:0,1,3,4,5,7,8,9,11,12,13,…,进而求出第2014个“好数”.
解答 解:(1)2014不是“好数”.如果2014是“好数”,不妨设2014=m2-n2(m,n为自然数),
则(m+n)(m-n)=2×1007,而m+n,m-n的奇、偶性相同,即(m+n)(m-n),要么是奇数要么能被4整除.
所以2014不是“好数”.
(2)设k为自然数,由(1)类似可得如4k+2的自然数都不是“好数”,
(k+1)2-(k-1)2=4k,(k+1)2-k2=2k+1,
故4k,2k+1的自然数都是“好数”,
所以从小到大的“好数”为:0,1,3,4,5,7,8,9,11,12,13,…
所以第n个“好数”为:n-1+[$\frac{n}{3}$],
所以第2014个“好数”为2684.
点评 此题主要考查了因式分解的应用,根据题意正确判断好数是解题关键.


科目:初中数学 来源: 题型:填空题
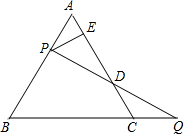 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论:
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OA,OB,OC是圆的三条半径.
如图,OA,OB,OC是圆的三条半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com