
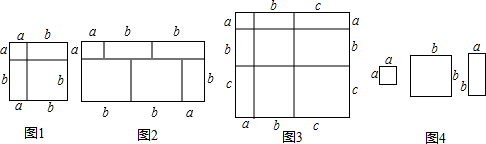
分析 (1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.
(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.
(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件
解答 解:(1)根据题意,大矩形的面积为:(a+2b)(a+b)=a2+3ab+2b2,
故答案为:(a+2b)(a+b)=a2+3ab+2b2.
(2)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,
各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,
∴等式为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故a2+b2+c2 =(a+b+c)2-2ab-2ac-2bc
=112-2×38
=45;
(3)(2a+b)(a+2b)=2a2+5ab+2b2;
如图所示:(答案不唯一)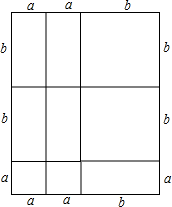 .
.
点评 本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
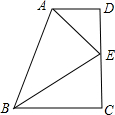 如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )
如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )| A. | AE⊥BE | B. | CE=DE | C. | AD+DE=BE | D. | AB=AD+BC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运往甲地 | 运往乙地 | |
| A | ||
| B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com