
分析 由a的值既是不等式组组$\left\{\begin{array}{l}{\frac{1}{3}x+1<2}\\{2(x+1)≤3x+4}\end{array}\right.$的解,又在函数y=$\frac{\sqrt{1-x}}{x}$的自变量取值范围内的有-1,-2,1,可直接利用概率公式求解即可求得答案.
解答 解:∵$\left\{\begin{array}{l}{\frac{1}{3}x+1<2}\\{2(x+1)≤3x+4}\end{array}\right.$的解是:-2≤x<3,
∴a的值既是不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1<2}\\{2(x+1)≤3x+4}\end{array}\right.$的解是:-2,-1,0,1,2,
∵y=$\frac{\sqrt{1-x}}{x}$的自变量取值范围为:$\left\{\begin{array}{l}{x≠0}\\{1-x≥0}\end{array}\right.$,
∴在函数y=$\frac{\sqrt{1-x}}{x}$的自变量取值范围内的有1,-1,-2,
∴a的值既是不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1<2}\\{2(x+1)≤3x+4}\end{array}\right.$的解,又在函数y=$\frac{\sqrt{1-x}}{x}$的自变量取值范围内的有:-1,-2,1,
∴a的值既是不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1<2}\\{2(x+1)≤3x+4}\end{array}\right.$的解,又在函数y=$\frac{\sqrt{1-x}}{x}$的自变量取值范围内的概率是$\frac{3}{5}$;
故答案为:$\frac{3}{5}$.
点评 本题考查的是随机事件概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
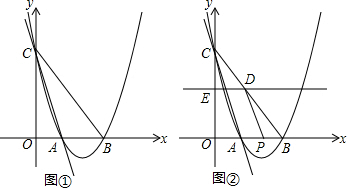
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
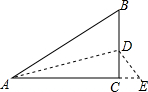 如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
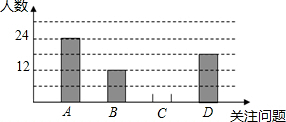 随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:
随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:| 关注问题 | 频数 | 频率 |
| A | 24 | B |
| B | 12 | 0.2 |
| C | N | 0.1 |
| D | 18 | M |
| 合计 | a | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com