
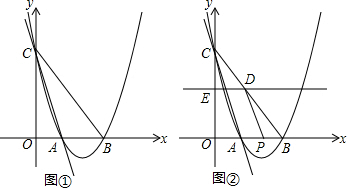
分析 (1)求出A、B两点坐标,可以设抛物线为y=a(x-2)(x-4),把点C坐标代入即可求出a.
(2)分两种情形①当△DBP∽△CBA时,$\frac{DB}{CB}$=$\frac{BP}{BA}$,②当△DBP∽△ABC时,$\frac{DB}{AB}$=$\frac{BP}{BC}$,列出方程即可解决.
(3)分三种情形①当DE=EP ②当DE=DP③当EP=DP,分别列出方程即可解决问题.
解答 解:(1)在y=-x+2中,令x=0,y=2;令y=0,x=2,得A(2,0),C(0,2),
又∵AB=2,
∴B(4,0),
∴设抛物线为y=a(x-2)(x-4),把C点坐标代入,得8a=2,a=$\frac{1}{4}$,
∴抛物线解析式为y=$\frac{1}{4}$x2-$\frac{3}{2}$x+2.
(2)∵AB=2,AC=2$\sqrt{2}$,BC=2$\sqrt{5}$.BP=2t,CE=t,
又∵DE∥x轴,
∴$\frac{CE}{CO}$=$\frac{CD}{CB}$,
∴$\frac{t}{2}$=$\frac{CD}{2\sqrt{5}}$,
∴CD=$\sqrt{5}$t,
∴DB=2$\sqrt{5}$-$\sqrt{5}$t.
当△DBP∽△CBA时,$\frac{DB}{CB}$=$\frac{BP}{BA}$,
∴$\frac{\sqrt{5}(2-t)}{2\sqrt{5}}$=$\frac{2t}{2}$,
∴t=$\frac{2}{3}$;
当△DBP∽△ABC时,$\frac{DB}{AB}$=$\frac{BP}{BC}$,
∴$\frac{\sqrt{5}(2-t)}{2}$=$\frac{2t}{2\sqrt{5}}$,
∴t=$\frac{10}{7}$.
(3)∵DE∥OB,
∴$\frac{DE}{OB}$=$\frac{CE}{CO}$,∵CE=t
∴DE=2t,
∵直线BC为y=-$\frac{1}{2}$x+2,
∴D(2t,-t+2),E(0,2-t),P(4-2t,0),
EP=$\sqrt{O{E}^{2}+O{P}^{2}}$=$\sqrt{5}$(2-t),DP=$\sqrt{(4-4t)^{2}+(2-t)^{2}}$;
①当DE=EP时,2t=-$\sqrt{5}$t+2$\sqrt{5}$,∴t=2$\sqrt{5}$($\sqrt{5}$-2)=10-4$\sqrt{5}$<2;
②当DE=DP时,4t2=t2-4t+4+16t2-32t+16,
13t2-36t+20=0,t1=$\frac{10}{13}$<2,t2=2(舍);
③当EP=DP时,5(2-t)2,=16(1-t)2+(2-t)2,
2-t=±2(1-t),
t1=$\frac{4}{3}$<2,t2=0(舍).
综上所述,符合条件的t值有:t1=10-4$\sqrt{5}$,t2=$\frac{10}{13}$,t3=$\frac{4}{3}$.
点评 本题考查二次函数、一次函数、勾股定理、平行线分线段成比例定理、相似三角形的判定和性质等知识,学会分类讨论的思想是解决问题的关键,学会转化的数学思想,利用相似三角形性质把问题转化为方程解决,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
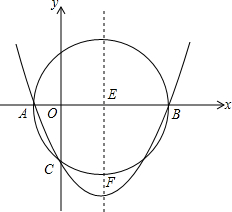 如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.
如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个三角形中至少有两个锐角 | |
| B. | 在同一平面内,垂直于同一直线的两条直线平行 | |
| C. | 同角的补角相等 | |
| D. | 如果a为实数,那么|a|>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com