
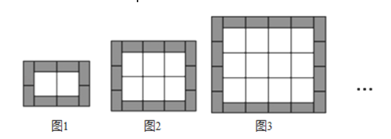
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:依据规律在第6个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)某新学校教室要装修,每间教室面积为68m2 , 准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
【答案】(1)28,42(2)每间教室瓷砖共需要5440元
【解析】
(1)通过观察发现规律得出黑色瓷砖的块数可用含n的代数式表示为4(n+1),白瓷砖的块数可用含n的代数式表示为n(n+1),然后将n=6代入计算即可;
(2)设白色瓷砖的行数为n,根据每间教室面积为68m2为等量关系列出方程,进而求解即可.
(1)通过观察图形可知,当n=1时,黑色瓷砖有8块,白瓷砖2块;
当n=2时,黑色瓷砖有12块,白瓷砖6块;
当n=3时,黑色瓷砖有16块,用白瓷砖12块;
则在第n个图形中,黑色瓷砖的块数可用含n的代数式表示为4(n+1),白瓷砖的块数可用含n的代数式表示为n(n+1),
当n=6时,黑色瓷砖的块数有4×(6+1)=28块,白色瓷砖有6×(6+1)=42块;
故答案为:28,42;
(2)设白色瓷砖的行数为n,根据题意,得:
0.52×n(n+1)+0.5×0.25×4(n+1)=68,
解得n1=15,n2=﹣18(不合题意,舍去),
白色瓷砖块数为n(n+1)=240,
黑色瓷砖块数为4(n+1)=64,
所以每间教室瓷砖共需要:20×240+10×64=5440元.
答:每间教室瓷砖共需要5440元.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:
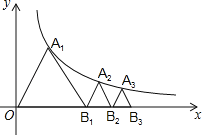
【题目】如图,已知等边△OA1B1,顶点A1在双曲线y=![]() (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是![]() 的直径,弦AB⊥CD于点G,直线EF与
的直径,弦AB⊥CD于点G,直线EF与![]() 相切与点D,则下列结论中不一定正确的是
相切与点D,则下列结论中不一定正确的是
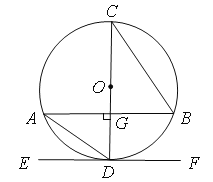
(A)AG=BG (B)AB∥EF (C)AD∥BC (D)∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=![]() .求证:CB是⊙O的切线.
.求证:CB是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
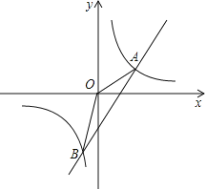
【题目】如图,一次函数![]() (
(![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() )的图象相交于A、B两点且点A的坐标为(2,1).
)的图象相交于A、B两点且点A的坐标为(2,1).
(1)分别求出一次函数与反比例函数的解析式以及点B的坐标;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线.
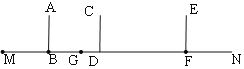
(1)请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法);
(2)求小明到达点F时的影长FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
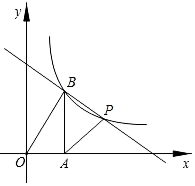
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋里装有2个相同的小球,它们分别写有数字1和2;乙口袋里装有3个相同的小球,它们分别写有数字3,4,5;丙口袋里有2个相同的小球,它们分别写有数字6,7,从三个口袋中各随机地取出1个小球,按要求解答下列问题:
(1)画出“树形图”;
(2)取出的3个小球上只有1个偶数数字的概率是多少?
(3)取出的3个小球上全是奇数数字的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com