
【题目】某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线.
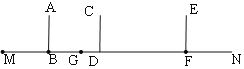
(1)请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法);
(2)求小明到达点F时的影长FH的长.
【答案】(1)(3分+2分)画图见解析;(2)FH的长为1.5米.
【解析】
试题本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.也考查了构建相似三角形,利用相似三角形的性质计算相应线段的长.
(1)连结MA、GC并延长MA和GC,它们相交于点O,然后连结OE并延长交MN于H,则FH为小明位于点F时在这个灯光下的影长;
(2)先利用速度公式得到BM=BD=3m,DF=4.5m,设AB=CD=EF=a,作OK⊥MN于K,如图,通过证明△MAB∽△MOK得到![]() =
=![]() ①,通过证明△GCD∽△GOK得到
①,通过证明△GCD∽△GOK得到![]() =
=![]() ②,由①②得
②,由①②得![]() =
=![]() ,可求出Dk=2,原式得到
,可求出Dk=2,原式得到![]() =
=![]() ,FK=DF-DK=2.5,然后证明△HEF∽△HOK,利用相似比可计算出HF.
,FK=DF-DK=2.5,然后证明△HEF∽△HOK,利用相似比可计算出HF.
试题解析:解:(1)如图,点O和FH为所作;
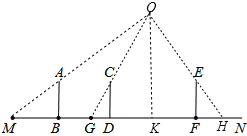
(2)BM=BD=2×1.5=3m,GD=1.2m,DF=1.5×1.5×2=4.5m,设AB=CD=EF=a,
作OK⊥MN于K,如图,
∵AB∥OK,
∴△MAB∽△MOK,
∴![]() =
=![]() ,即
,即![]() =
=![]() ①,
①,
∵CD∥OK,
∴△GCD∽△GOK,
∴CDOK=GDGK,即![]() =
=![]() ②,
②,
由①②得![]() =
=![]() ,解得Dk=2,
,解得Dk=2,
∴![]() =
=![]() =
=![]() ,FK=DF-DK=4.5-2=2.5,
,FK=DF-DK=4.5-2=2.5,
∵EF∥OK,
∴△HEF∽△HOK,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴HF=1.5(m).
答:小明到达点F时的影长FH的长为1.5m.


科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 为反比例函数.
为反比例函数.
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)求出﹣2≤x≤﹣![]() 时,y的取值范围.
时,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(CD)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(EF)1.6米,求旗杆的高度AB.
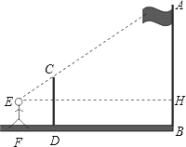
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:依据规律在第6个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)某新学校教室要装修,每间教室面积为68m2 , 准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
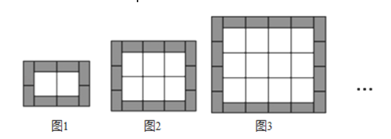
查看答案和解析>>
科目:初中数学 来源: 题型:
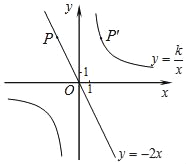
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求反比例函数的解析式;
(2)直接写出当y<4时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
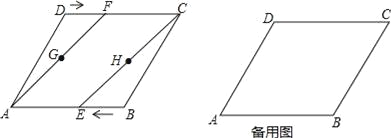
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞安市文化创意实践学校是一所负责全市中小学生素质教育综合实践活动的公益类事业单位,学校目前可开出:创意手工创意表演、科技制作(创客)、文化传承、户外拓展等5个类别20多个项目课程.
(1)学校3月份接待学生1000人,5月份增长到2560人,求该学校接待学生人数的平均月增长率是多少?
(2)在参加“创意手工”体验课程后,小明发动本校同学将制作的作品义卖募捐.当作品卖出的单价是2元时,每天义卖的数量是150件;当作品的单价每涨高1元时,每天义卖的数量将减少10件.问:在作品单价尽可能便宜的前提下,当单价定为多少元时,义卖所得的金额为600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
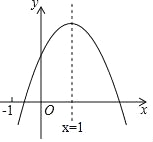
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(x1,0),且﹣1<x1<0,对称轴x=1.如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中所有结论正确的是______(填写番号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com