
【题目】如图,CD是![]() 的直径,弦AB⊥CD于点G,直线EF与
的直径,弦AB⊥CD于点G,直线EF与![]() 相切与点D,则下列结论中不一定正确的是
相切与点D,则下列结论中不一定正确的是
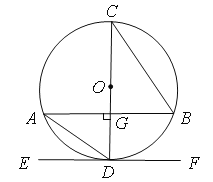
(A)AG=BG (B)AB∥EF (C)AD∥BC (D)∠ABC=∠ADC
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F.若BF=2,AF=3,则△ABC的面积是( )
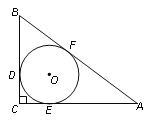
A. 6 B. 7 C. 12 D. 7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知a=3,b和c是关于x的方程x2+mx+2-![]() m=0的两个实数根.
m=0的两个实数根.
(1)求△ABC的周长.
(2)求△ABC的三边均为整数时的外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
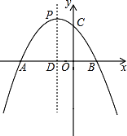
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0 的两根 x1,x2均为正数,其中x1>x2,且满足1<x1﹣x2<2,那么称这个方程有“友好根”.
(1)方程(x﹣![]() )(x﹣
)(x﹣![]() )=0_____“友好根”(填:“有”或“没有”);
)=0_____“友好根”(填:“有”或“没有”);
(2)已知关于x的 x2﹣(t﹣1)x+t﹣2=0有“友好根”,求 t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向 A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二: 同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受 9 折优惠的概率为_______;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
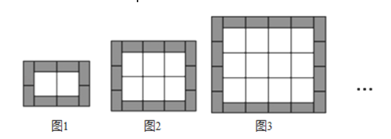
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:依据规律在第6个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)某新学校教室要装修,每间教室面积为68m2 , 准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点(含端点
上的动点(含端点![]() ,
,![]() ),连结
),连结![]() ,以
,以![]() 所在直线为对称轴作点
所在直线为对称轴作点![]() 的对称点
的对称点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,连结
的中点,连结![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(3)以![]() 其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com