
【题目】在平面直角坐标系![]() 中,将
中,将![]() (
(![]() )沿直线
)沿直线![]() 运动到点
运动到点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则称点
,则称点![]() 为点
为点![]() 的“铅直变换点”。
的“铅直变换点”。
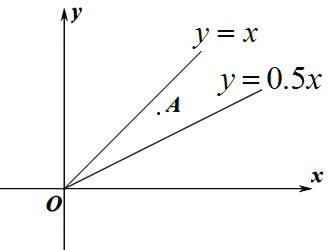
(1) 点![]() 的铅直变换点坐标___________;一个点的铅直变换点是
的铅直变换点坐标___________;一个点的铅直变换点是![]() ,则这个点的坐标_________
,则这个点的坐标_________
(2) 已知点![]() 的坐标为(
的坐标为(![]() ). 点
). 点![]() 在一次函数
在一次函数![]() 的图像上,点
的图像上,点![]() 的铅直变换点为点
的铅直变换点为点![]() ,若这三个点中,其中的两个点关于另一点成中心对称,求
,若这三个点中,其中的两个点关于另一点成中心对称,求![]() 的值.
的值.
(3) 已知点![]() 在一次函数
在一次函数![]() 和一次函数
和一次函数![]() 的图像所组成的角的内部,它的铅直变换点为点B,且
的图像所组成的角的内部,它的铅直变换点为点B,且![]() 满足
满足![]() ,判断线段
,判断线段![]() 的长度能否等于
的长度能否等于![]() ,若能,求点
,若能,求点![]() 的坐标,若不能,请说明理由。
的坐标,若不能,请说明理由。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ; (3) 不能
; (3) 不能
【解析】
(1)根据“铅直变换点”的定义即可求解;
(2)根据“铅直变换点”的定义写出B点坐标,再根据中心对称的特点分情况讨论;
(3)根据A点处于夹角内部得到![]() <b<a,得到a-b>0,B点坐标为(a,a-b),根据
<b<a,得到a-b>0,B点坐标为(a,a-b),根据![]() =a-b得到
=a-b得到![]() <
<![]() ,求出a的取值,再得到b>a-b,从而得到AB的长度,根据
,求出a的取值,再得到b>a-b,从而得到AB的长度,根据![]() 的长度为
的长度为![]() 得到a,b之间的关系,再代入
得到a,b之间的关系,再代入![]() ,根据根的判别式即可求解.
,根据根的判别式即可求解.
(1)点![]() 的铅直变换点坐标为(4,4-3),即为
的铅直变换点坐标为(4,4-3),即为![]() ;
;
一个点的铅直变换点是![]() ,即
,即![]() ,则这个点的坐标为
,则这个点的坐标为![]() ;
;
故填:![]() ,
,![]() ;
;
(2)∵点![]() 的坐标为(
的坐标为(![]() ). 点
). 点![]() 在一次函数
在一次函数![]() 的图像上,
的图像上,
∴点![]() (a,b+1),∴A的铅直变换点为点
(a,b+1),∴A的铅直变换点为点![]() (a,1),
(a,1),
①若A,B关于C成中心对称,则![]()
解得a=![]()
②若C,B关于A成中心对称,则![]()
解得a=3
③若A,C关于B成中心对称,则![]()
解得a=![]()
故![]() 时这三个点中,其中的两个点关于另一点成中心对称;
时这三个点中,其中的两个点关于另一点成中心对称;
(3)不能,理由如下:
根据A点处于夹角内部得到![]() <b<a,
<b<a,
∴a-b>0,
∵A(a,b)
∴B点坐标为(a,a-b),
∵![]() ,
,
∴a-b=![]() ,
,
∵![]() <b
<b
∴a-![]() <b
<b
∴a-b<![]()
即![]() <
<![]()
故a(2a-1)<0,
根据二次函数图像可得a的取值为0<a<![]() ;
;
又![]() <b<a,
<b<a,
∴b>a-b,
故AB=b-(a-b)=2b-a= ![]()
得到b=![]()
代入![]() ,得
,得![]()
△=16-4×8=-16<0,
故a无解,即![]() 的长度不能等于
的长度不能等于![]() .
.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )
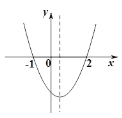
A.函数有最小值B.图象对称轴是直线x=![]()
C.当x<![]() ,y随x的增大而减小D.当-1<x<2时,y>0
,y随x的增大而减小D.当-1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
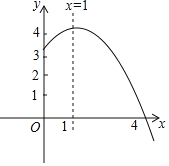
【题目】抛物线![]() 的部分图象如图所示,与
的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() 。给出下列结论:①
。给出下列结论:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为
有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为![]() ,其中正确的结论有。其中正确的有_____________。(只需填写序号即可)
,其中正确的结论有。其中正确的有_____________。(只需填写序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
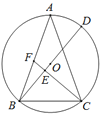
【题目】如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.
(1)求证:∠BFC=∠ABC.
(2)若⊙O的半径为5,CF=6,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
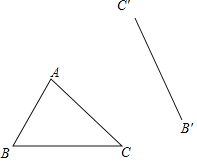
【题目】如图,求作△ABC绕某点旋转一定角度后的△A′B′C′时,某同学只作了一部分图形.
(1)请把△A′B′C′作完整,并保留作图痕迹;
(2)写出基本作图步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,其对称轴为x=1,有下列结论:①abc<0;②b<a+c;③4a+2b+c<0;④a+b≥m(am+b),其中正确的结论有( )

A.①②B.②③C.①④D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com