
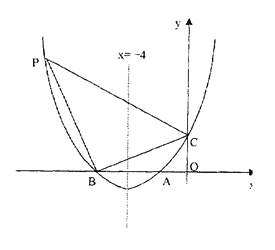
【题目】如图,已知抛物线的对称轴是x=-4,抛物线与x轴交于A,B两点,与y轴交于C点,O是坐标原点,且A,C的坐标分别是(-2,0),(0,3).
(1)求抛物线的解析式;
(2)抛物线上有一点是P,满足∠PBC=90,求P点的坐标;
(3)y轴上是否存在点E使得△AOE与△PBC相似?若存在求出点E的坐标,若不存在,请说明理由.
【答案】(1)y=![]() x2+2x+3 ;(2)(-10,8);(3)(0,
x2+2x+3 ;(2)(-10,8);(3)(0,![]() )和(0,-
)和(0,-![]() ).
).
【解析】
根据对称性写出B点坐标,再设参数解方程求得抛物线解析式;利用相似三角形的判定及性质定理及抛物线解析式解出P坐标;第三问同样借助相似三角形性质定理解答.
(1)抛物线的对称轴是x=-4,A的坐标是(-2,0),则B坐标为(-6,0),设![]() ,把AB两点坐标带入得:
,把AB两点坐标带入得:![]() ,解得
,解得 ,抛物线解析式为 y=
,抛物线解析式为 y=![]() x2+2x+3;(2)过P作PF
x2+2x+3;(2)过P作PF![]() ,所以
,所以![]() ,从而
,从而![]() ,又OB=6,OC=3,故PF=2BF,设BF=m则PF=2m,OF=6+m,P坐标为(-6-m,2m),由点P在抛物线上可得2m=
,又OB=6,OC=3,故PF=2BF,设BF=m则PF=2m,OF=6+m,P坐标为(-6-m,2m),由点P在抛物线上可得2m=![]() ,解得m1=0(舍去),m2=4,故P(-10,8);(3)设E坐标为(0,n),由已知得BC=
,解得m1=0(舍去),m2=4,故P(-10,8);(3)设E坐标为(0,n),由已知得BC=![]() ,PB=4
,PB=4![]() ,若△AOE
,若△AOE![]() △PBC,则
△PBC,则![]() ,
,![]() ,n=
,n=![]() ,所以存在E点,E点坐标为(0,
,所以存在E点,E点坐标为(0,![]() )和(0,-
)和(0,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,m)和点B(n,0)分别在y轴和x轴的正半轴上,满足![]() ,连接线段AB,点C为AB上一动点.
,连接线段AB,点C为AB上一动点.
(1)填空:m=_____,n=_____;
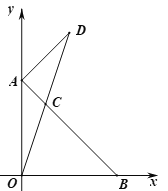
(2)如图,连接OC并延长至点D,使得DC=OC,连接AD.若△AOC的面积为2,求点D的坐标;
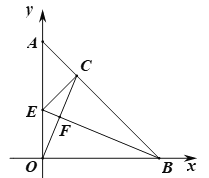
(3)如图,BC=OB,∠ABO的平分线交线段AO于点E,交线段OC于点F,连接EC.
求证:①△ACE为等腰直角三角形;
②BF-EF=OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与一次函数y=-2x+m的图象交于A、B两点,AC⊥x轴于C, △AOC的面积为3.
与一次函数y=-2x+m的图象交于A、B两点,AC⊥x轴于C, △AOC的面积为3.
(1)根据这些条件,试确定反比例函数的解析式;
(2)根据这些条件,你能求出一次函数的关系式吗?如果能请你求出来;如果不能,请你添加一个条件,求出一次函数的关系式.(注意:不能添加m的值);
(3)根据你所求出的一次函数的关系式,求出△AOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b经过点A(0,3)和点B(4,a),且点B在正比例函数y=![]() x的图象上.
x的图象上.
(1)求a的值.
(2)求k和b的值,并在给定的坐标系内画出这条直线.
(3)如果点C(![]()
![]() ,y1)和点D(﹣
,y1)和点D(﹣![]() ,y2)都在这条直线上,请比较y1和y2的大小.
,y2)都在这条直线上,请比较y1和y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,点
,点![]() 在该函数的图象上,点
在该函数的图象上,点![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .设
.设![]() ,下列结论中:
,下列结论中:
①![]() 没有最大值;②
没有最大值;②![]() 没有最小值;③
没有最小值;③![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④满足![]() 的点
的点![]() 有四个.其中正确结论的个数有( )
有四个.其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 经过点
经过点![]() 和点
和点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() ,则:①
,则:①![]() ;②无论
;②无论![]() 取何值,此二次函数图象与
取何值,此二次函数图象与![]() 轴必有两个交点,函数图象截
轴必有两个交点,函数图象截![]() 轴所得的线段长度必大于
轴所得的线段长度必大于![]() ;③当函数在
;③当函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;④当
的增大而减小;④当![]() 时,
时,![]() ;⑤若
;⑤若![]() ,则
,则![]() .以上说法正确的有( )
.以上说法正确的有( )
A. ①②③④⑤ B. ①②④⑤ C. ②③④ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com