
【题目】在平面直角坐标系中,点A(0,m)和点B(n,0)分别在y轴和x轴的正半轴上,满足![]() ,连接线段AB,点C为AB上一动点.
,连接线段AB,点C为AB上一动点.
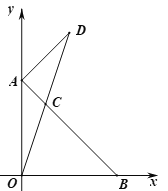
(1)填空:m=_____,n=_____;
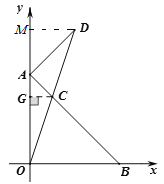
(2)如图,连接OC并延长至点D,使得DC=OC,连接AD.若△AOC的面积为2,求点D的坐标;
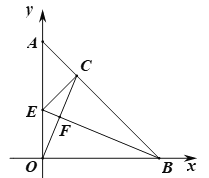
(3)如图,BC=OB,∠ABO的平分线交线段AO于点E,交线段OC于点F,连接EC.
求证:①△ACE为等腰直角三角形;
②BF-EF=OC.
【答案】(1)4,4;(2)D(2,6);(3)①见解析;②见解析.
【解析】
(1)根据非负数的性质可得关于m、n的方程组,解方程组即可求出m、n的值;
(2)过点C作CG⊥y轴于点G,过点D作DM⊥y轴于点M,如图,由题意易得△AOB和△ACG均为等腰直角三角形,由△AOC的面积为2可求得AG的长,进而可求出OG的长,再利用三角形的中位线可得DM和OM的长,即得点D的坐标;
(3)①先利用SAS证明△OBE≌△CBE,可得∠BCE=∠BOA=90°,再根据∠OAB =45°和三角形的内角和求出∠AEC的度数,进一步即可证得结论;
②过点A作AH⊥OC交OC的延长线于点H,如图,根据AAS可证明△ACH≌△CEF,从而得EF=CH,同理可证△AOH≌△OBF,得OH=BF,问题即得解决.
解:(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
故答案为4,4;
(2)由(1)得,A(0,4)、B(4,0),∴OA=OB=4,∵∠BOA=90°,∴∠OAB=∠OBA=45°,
过点C作CG⊥y轴于点G,过点D作DM⊥y轴于点M,如图,
则CG∥DM,∠ACG=45°,∴AG=CG,
∵△AOC的面积为2,∴![]() ,解得:CG=1,
,解得:CG=1,
∴AG=1,∴OG=3,
∵C是OD的中点,CG∥DM,
∴DM=2CG=2,OM=2OG=6,
∴点D的坐标是(2,6);
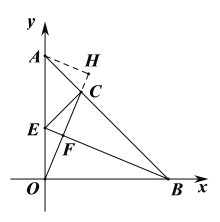
(3)①证明:∵BE平分∠ABO,∴∠OBE=∠CBE,
又∵OB=CB,BE=BE,
∴△OBE≌△CBE(SAS),∴∠BCE=∠BOA=90°,即∠ACE=90°,
∵∠OAB =45°,∴∠AEC=45°,
∴ ∠AEC=∠CAE,∴CA=CE,
∴△ACE为等腰直角三角形;
②过点A作AH⊥OC交OC的延长线于点H,如图,
∵BC=BO,BE平分∠ABO,∴BF⊥OC,
∴∠AHC=∠CFE=90°,
∵∠CAH+∠ACH=90°,∠ECF+∠ACH=90°,
∴∠CAH=∠ECF,又∵AC=CE,
∴△ACH≌△CEF(AAS),∴EF=CH,
同理可证:△AOH≌△OBF(AAS),
∴OH=BF,
∴OC+EF=BF,即BF-EF=OC.


科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的边长是4,∠ABC=120°,点M、N分别在边AD、AB上,且MN⊥AC,垂足为P,把△AMN沿MN折叠得到△AˊMN,若△AˊDC恰为等腰三角形,则AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
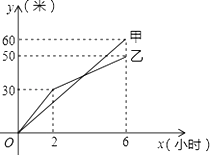
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲种污水处理器处理25吨的污水与乙种污水处理器处理35吨的污水所用的时间相同,已知乙种污水处理器每小时比甲种污水处理器多处理20吨的污水.
(1)分别求甲、乙两种污水处理器的污水处理效率;
(2)若某厂每天同时开甲、乙两种污水处理器处理污水共4小时,且甲、乙两种污水处理器处理污水每吨需要的费用分别30元和50元,问该厂每个月(以30天计)需要污水处理费多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的对称轴是x=-4,抛物线与x轴交于A,B两点,与y轴交于C点,O是坐标原点,且A,C的坐标分别是(-2,0),(0,3).
(1)求抛物线的解析式;
(2)抛物线上有一点是P,满足∠PBC=90,求P点的坐标;
(3)y轴上是否存在点E使得△AOE与△PBC相似?若存在求出点E的坐标,若不存在,请说明理由.
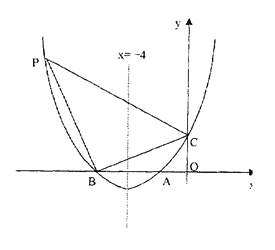
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com