
����Ŀ��������ˮ����������25�ֵ���ˮ��������ˮ����������35�ֵ���ˮ���õ�ʱ����ͬ����֪������ˮ������ÿСʱ�ȼ�����ˮ�������ദ��20�ֵ���ˮ��
��1���ֱ���ס���������ˮ����������ˮ����Ч�ʣ�
��2����ij��ÿ��ͬʱ���ס���������ˮ������������ˮ��4Сʱ���Ҽס���������ˮ������������ˮÿ����Ҫ�ķ��÷ֱ�30Ԫ��50Ԫ���ʸó�ÿ���£���30��ƣ���Ҫ��ˮ�����Ѷ��٣�
���𰸡���1��������ˮ������ÿСʱ������ˮ50�֣�������ˮ������ÿСʱ������ˮ70�֣���2���ó�ÿ���£���30��ƣ���Ҫ��ˮ������600000Ԫ��
��������
��1�������������ˮ������ÿСʱ������ˮx�֣�����������ˮ������ÿСʱ������ˮ��x+20���֣���������ɵõ�����ϵ��������ˮ����������25�ֵ���ˮ��������ˮ����������35�ֵ���ˮ����ʱ�䣬���ݵ�����ϵ���г����̣��ٽ⼴�ɣ�
��2�����������г�����ʽ���ɣ�
�⣺��1���������ˮ������ÿСʱ������ˮx�֣�������ã�
![]() ��
��
��֮�ã�x��50��
�����飬x��50��ԭ���̵Ľ⣬����x��50��
x+20��70��
�𣬼�����ˮ������ÿСʱ������ˮ50�֣�������ˮ������ÿСʱ������ˮ70�֣�
��2��30��4��50��30+30��4��70��50��180000+420000��600000��Ԫ����
�𣺸ó�ÿ���£���30��ƣ���Ҫ��ˮ������600000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ�����C������CM�������ACM=��ABC��
��1���ж�CM���O��λ�ù�ϵ����֤����
��2���ӳ�BC��D��ʹBC=CD������AD��CM���ڵ�E������O�İ뾶Ϊ3��ED=2������ACE�����Բ�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2��2��3��4�ĸ��������ȡ����������һ����Ϊ��λ�ϵ����֣��ڶ�����Ϊʮλ�ϵ����֣����һ����λ�����������λ����2�ı����ĸ����� �� ��
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A(0,m)�͵�B(n,0)�ֱ���y���x����������ϣ�����![]() �������߶�AB����CΪAB��һ����.
�������߶�AB����CΪAB��һ����.
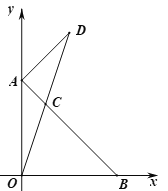
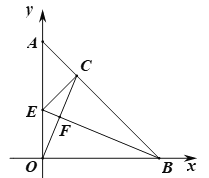
(1)���:m=_____��n=_____��
(2)��ͼ������OC���ӳ�����D��ʹ��DC=OC������AD.����AOC�����Ϊ2�����D�����ꣻ
(3)��ͼ��BC=OB����ABO��ƽ���߽��߶�AO�ڵ�E�����߶�OC�ڵ�F������EC.
��֤���١�ACEΪ����ֱ��������;
��BF��EF=OC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��AB��![]() �ֱ���x��y�ύ��A��B���㣬����B��ֱ�߽�x���������ڵ�C����OB��OC=3��1.
�ֱ���x��y�ύ��A��B���㣬����B��ֱ�߽�x���������ڵ�C����OB��OC=3��1.
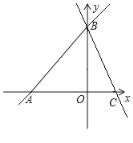
��1��ֱ��д����A��B��C�����ꣻ
��2�����߶�OB�ϴ��ڵ�P��ʹ��P��B��C�ľ�����ȣ������P�����ꣻ
��3����x���Ϸ����ڵ�D��ʹ���Ե�A��B��DΪ��������������ABCȫ�ȣ������D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����������y=![]() ��һ�κ���y=-2x+m��ͼ����A��B����,AC��x����C, ��AOC�����Ϊ3.
��һ�κ���y=-2x+m��ͼ����A��B����,AC��x����C, ��AOC�����Ϊ3.
(1)������Щ����,��ȷ�������������Ľ���ʽ;
(2)������Щ����,�������һ�κ����Ĺ�ϵʽ��?��������������;�������,��������һ������,���һ�κ����Ĺ�ϵʽ.(ע��:��������m��ֵ);
(3)�������������һ�κ����Ĺ�ϵʽ,�����AOD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y��kx+b������A��0��3���͵�B��4��a�����ҵ�B������������y��![]() x��ͼ���ϣ�
x��ͼ���ϣ�
��1����a��ֵ��
��2����k��b��ֵ�����ڸ���������ϵ�ڻ�������ֱ�ߣ�
��3�������C��![]()
![]() ��y1���͵�D����
��y1���͵�D����![]() ��y2����������ֱ���ϣ���Ƚ�y1��y2�Ĵ�С��
��y2����������ֱ���ϣ���Ƚ�y1��y2�Ĵ�С��
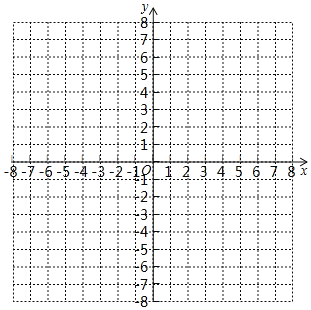
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»��̳�����ij�ֱ��䣬ÿ̨����Ϊ2500Ԫ�����ۼ�Ϊ2900Ԫ��ƽ��ÿ�����۳�8̨�����鷢�֣������ۼ�ÿ����50Ԫ��ƽ��ÿ����ܶ��۳�4̨���̳�Ҫ��ʹ���ֱ������������ƽ��ÿ��ﵽ5000Ԫ��ÿ̨����Ӧ�ý��۶���Ԫ������ÿ̨���併��xԪ������������з��̣�������
A. (2900-x)(8+4��![]() )=5000 B. (400-x)(8+4��
)=5000 B. (400-x)(8+4��![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC����һ�㣬��D��E��F�ֱ�ΪOA��OB��OC���е㣬��ͼ��������������( )

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com