
【题目】如图,![]() 平分
平分![]() ,且
,且![]() .
.
(1)在图1中,当![]() 时,求证:
时,求证:![]() ;
;
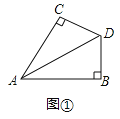
(2)在图2中,当![]() 时,求证:
时,求证:![]() .
.
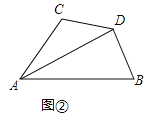
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,m)和点B(n,0)分别在y轴和x轴的正半轴上,满足![]() ,连接线段AB,点C为AB上一动点.
,连接线段AB,点C为AB上一动点.
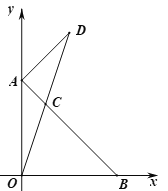
(1)填空:m=_____,n=_____;
(2)如图,连接OC并延长至点D,使得DC=OC,连接AD.若△AOC的面积为2,求点D的坐标;
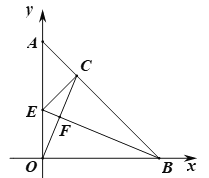
(3)如图,BC=OB,∠ABO的平分线交线段AO于点E,交线段OC于点F,连接EC.
求证:①△ACE为等腰直角三角形;
②BF-EF=OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 经过点
经过点![]() 和点
和点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() ,则:①
,则:①![]() ;②无论
;②无论![]() 取何值,此二次函数图象与
取何值,此二次函数图象与![]() 轴必有两个交点,函数图象截
轴必有两个交点,函数图象截![]() 轴所得的线段长度必大于
轴所得的线段长度必大于![]() ;③当函数在
;③当函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;④当
的增大而减小;④当![]() 时,
时,![]() ;⑤若
;⑤若![]() ,则
,则![]() .以上说法正确的有( )
.以上说法正确的有( )
A. ①②③④⑤ B. ①②④⑤ C. ②③④ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为![]() 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每上涨
件,而销售单价每上涨![]() 元,就会少售出
元,就会少售出![]() 件玩具,超市要完成不少于
件玩具,超市要完成不少于![]() 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )

A. 1对 B. 2对 C. 3对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点![]() .
.
![]() 写出函数表达式;
写出函数表达式;
![]() 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限?![]() 随
随![]() 的增大怎样变化?
的增大怎样变化?
![]() 点
点![]() 、
、![]() 在这个函数的图象上吗?
在这个函数的图象上吗?
![]() 如果点
如果点![]() 在图象上,求
在图象上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com