
【题目】已知关于![]() 的方程
的方程![]() ,
,![]() ,
,![]() 是此方程的两个根,现给出三个结论:①
是此方程的两个根,现给出三个结论:①![]() ;②
;②![]() ;③
;③![]() ,则结论正确结论号是________(填上你认为正确结论的所有序号)
,则结论正确结论号是________(填上你认为正确结论的所有序号)
【答案】①②
【解析】
(1)可以利用方程的判别式就可以判定是否正确;
(2)根据两根之积就可以判定是否正确;
(3)利用根与系数的关系可以求出x12+x22的值,然后也可以判定是否正确.
①∵方程x2﹣(a+b)x+ab﹣1=0中,△=(a+b)2﹣4(ab﹣1)=(a﹣b)2+4>0,∴x1≠x2,故①正确;
②x1x2=ab﹣1<ab,故②正确;
③∵x1+x2=a+b,即(x1+x2)2=(a+b)2,∴x12+x22=(x1+x2)2﹣2x1x2=(a+b)2﹣2ab+2=a2+b2+2>a2+b2,即x12+x22>a2+b2.故③错误;
综上所述:正确的结论序号是:①②.
故答案为:①②.


科目:初中数学 来源: 题型:
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小津去某风景区游览.小明从明桥出发沿景区公路骑自行车去陶公亭,同一时刻小津在霞山乘电动汽车出发沿同一公路去陶公亭,车速为![]() .他们出发后
.他们出发后![]() 时,离霞山的路程为
时,离霞山的路程为![]() ,
,![]() 为
为![]() 的函数图象如图所示.
的函数图象如图所示.
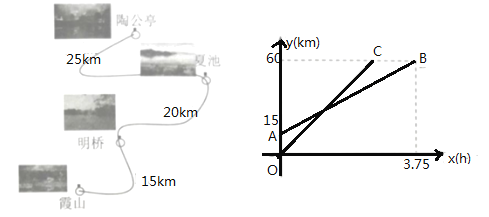
(1)求直线![]() 和直线
和直线![]() 的函数表达式;
的函数表达式;
(2)回答下列问题,并说明理由:
①当小津追上小明时,他们是否已过了夏池?
②当小津到达陶公亭时,小明离陶公亭还有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于A,B两点,点
与x轴,y轴分别交于A,B两点,点![]() 为直线
为直线![]() 上一点,直线
上一点,直线![]() 过点C.
过点C.

![]() 求m和b的值;
求m和b的值;
![]() 直线
直线![]() 与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动
与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动![]() 设点P的运动时间为t秒.
设点P的运动时间为t秒.
①若点P在线段DA上,且![]() 的面积为10,求t的值;
的面积为10,求t的值;
②是否存在t的值,使![]() 为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
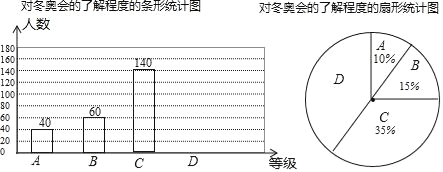
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
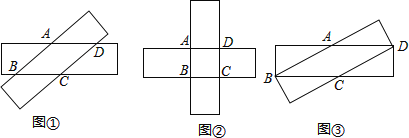
【题目】小宇将两张长为8宽为2的矩形条交叉如图①,发现重叠部分可能是一个菱形.
(1)请你帮助小宇证明四边形ABCD是菱形.
(2)小宇又发现:如图②时,菱形ABCD的周长最小,等于 ;
(3)如图③时菱形ABCD的周长最大,求此时菱形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com