
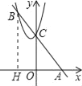
【题目】已知:如图所示,一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点,二次函数y=x2+bx+c的图象过点C,且与一次函数在第二象限交于另一点B,若AC:CB=1:2,那么这二次函数的顶点坐标为_____.
【答案】(﹣![]() ,
,![]() ).
).
【解析】
由一次函数y=﹣2x+3可求出A、C两点的坐标,再根据B也在此直线上,可设出B点坐标,由AC:CB=1:2可知B点坐标,把B、C点坐标代入二次函数的解析式可求出b、c的值,从而求出其解析式及顶点坐标.
∵一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点,∴令x=0,得:y=3,令y=0,得:x=![]() ,∴A(
,∴A(![]() ,0),C(0,3),因为点B在直线y=﹣2x+3的图象上,所以设B点(x,﹣2x+3).
,0),C(0,3),因为点B在直线y=﹣2x+3的图象上,所以设B点(x,﹣2x+3).
∵AC:CB=1:2,∴CB=2AC,∴![]() =2
=2![]() ,则x2=9,解得:x=3(舍去),x=﹣3,∴x=﹣3.
,则x2=9,解得:x=3(舍去),x=﹣3,∴x=﹣3.
把B(﹣3,9)C(0,3)代入二次函数解析式得:![]() ,解得:
,解得:![]() ,故二次函数的解析式为y=x2+x+3.
,故二次函数的解析式为y=x2+x+3.
∵y=x2+x+3=![]() ,故顶点坐标为(﹣
,故顶点坐标为(﹣![]() ).
).
故答案为:(﹣![]() ).
).


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() ,
,![]() ,
,![]() 垂足分别为
垂足分别为![]() 、
、![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 在射线
在射线![]() 上运动.它们运动的时间为
上运动.它们运动的时间为![]() (当点
(当点![]() 运动结束时,点
运动结束时,点![]() 运动随之结束).
运动随之结束).
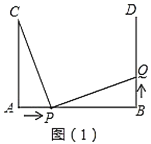
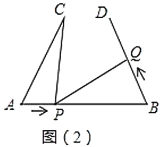
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,
时,![]() 与
与![]() 是否全等,并判断此时线段
是否全等,并判断此时线段![]() 和线段
和线段![]() 的位置关系,请分别说明理由;
的位置关系,请分别说明理由;
(2)如图(2),若“![]() ,
,![]() ”改为“
”改为“![]() ”,点
”,点![]() 的运动速度为
的运动速度为![]() ,其它条件不变,当点
,其它条件不变,当点![]() 、
、![]() 运动到何处时有
运动到何处时有![]() 与
与![]() 全等,求出相应的
全等,求出相应的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=ax2+bx+c的图象有下列命题,其中是假命题的个数是( )
①当c=0时,函数的图象经过原点;
②当b=0时,函数的图象关于y轴对称;
③函数的图象最高点的纵坐标是![]() ;
;
④当c>0且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
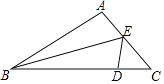
(1)求证:AE=DE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等边三角形,点P是BC上一动点(点P与点B、C不重合),过点P作PM∥AC交AB于M,PN∥AB交AC于N,连接BN、CM.
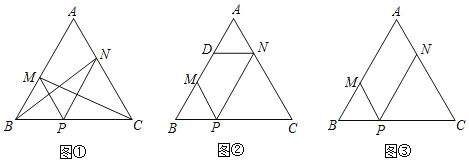
(1)求证:PM+PN=BC;
(2)在点P的位置变化过程中,BN=CM是否成立?试证明你的结论;
(3)如图②,作ND∥BC交AB于D,则图②成轴对称图形,类似地,请你在图③中添加一条或几条线段,使图③成轴对称图形(画出一种情形即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
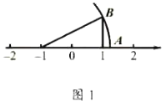
【题目】(1)如图1,![]() 中,
中,![]() ,点
,点![]() 在数轴-1处,点
在数轴-1处,点![]() 在数轴1处,
在数轴1处,![]() ,
,![]() ,则数轴上点
,则数轴上点![]() 对应的数是 .
对应的数是 .
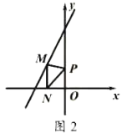
(2)如图2,点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上的动点,当以
轴上的动点,当以![]() ,
,![]() ,
,![]() 为顶点的三角形为等腰直角三角形时点
为顶点的三角形为等腰直角三角形时点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com