
【题目】如图①,△ABC是等边三角形,点P是BC上一动点(点P与点B、C不重合),过点P作PM∥AC交AB于M,PN∥AB交AC于N,连接BN、CM.
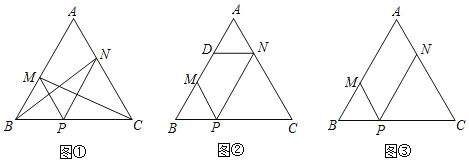
(1)求证:PM+PN=BC;
(2)在点P的位置变化过程中,BN=CM是否成立?试证明你的结论;
(3)如图②,作ND∥BC交AB于D,则图②成轴对称图形,类似地,请你在图③中添加一条或几条线段,使图③成轴对称图形(画出一种情形即可).
【答案】(1)见解析;(2)结论成立,理由见解析;(3)见解析
【解析】
(1)先证明△BMP,△CNP是等边三角形,再证明△BPN≌△MPC,从而PM=PB,PN=PC,可得PM+PN=BC;
(2)BN=CM总成立,由(1)知△BPN≌△MPC,根据全等三角形的性质可得结论;
(3)作ND∥BC交AB于N,作ME∥BC交AC于M,作EF∥AB交BC于F,连接DF即可.
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∵PM∥AC,PN∥AB,
∴∠BPM=∠ACB=60°,∠CPN=∠ABC=60°,
∴△BMP,△CNP是等边三角形,
∴∠BPM=∠CPN=60°,PN=PC,PN=PC,
∴∠BPN=∠MPC,
∴△BPN≌△MPC,
∴PM=PB,PN=PC,
∵BP+PC=BC,
∴PM+PN=BC;
(2)BN=CM总成立,理由:
由(1)知△BPN≌△MPC,
∴BN=CM;
(3)解:如图③即为所求.
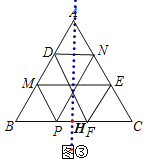
作ND∥BC交AB于N,作ME∥BC交AC于M,作EF∥AB交BC于F,连接DF,作直线AH⊥BC交BC于H,
同(1)可证△AND,△AME,△BPM,△CEF都是等边三角形,
∴D与N,M与E,B与C关于AH对称.
∴BM=CE,
∴BM=CF,
∴P与F关于AH对称,
∴所做图形是轴对称图形.


科目:初中数学 来源: 题型:
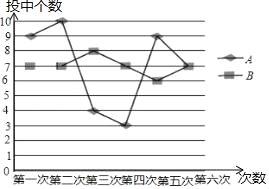
【题目】某班为确定参加学校投篮比赛的任选,在A、B两位投篮高手间进行了6次投篮比赛,每人每次投10个球,将他们每次投中的个数绘制成如图所示的折线统计图.
(1)根据图中所给信息填写下表:
投中个数统计 | 平均数 | 中位数 | 众数 |
A |
| 8 |
|
B | 7 |
| 7 |
(2)如果这个班只能在A、B之间选派一名学生参赛,从投篮稳定性考虑应该选派谁?请你利用学过的统计量对问题进行分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场用如图1所示的同一种地砖拼图案,第一次拼成的图案如图2所示,共用地砖4块;第2次拼成的图案如图3所示,共用地砖![]() ;第3次拼成的图案如图4所示,共用地砖
;第3次拼成的图案如图4所示,共用地砖![]() ,….
,….
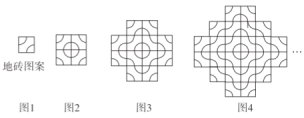
(1)直接写出第4次拼成的图案共用地砖________块;
(2)按照这样的规律,设第![]() 次拼成的图案共用地砖的数量为
次拼成的图案共用地砖的数量为![]() 块,求
块,求![]() 与
与![]() 之间的函数表达式
之间的函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点,二次函数y=x2+bx+c的图象过点C,且与一次函数在第二象限交于另一点B,若AC:CB=1:2,那么这二次函数的顶点坐标为_____.
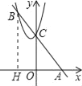
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象抛物线G经过(﹣5,0),(0,![]() ),(1,6)三点,直线l的解析式为y=2x﹣3
),(1,6)三点,直线l的解析式为y=2x﹣3
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=![]() 与y轴交于(0,3)点.
与y轴交于(0,3)点.
(1)求出m的值并在给出的直角坐标系中画出这条抛物线;
(2)根据图像回答下列问题:
①方程![]() 的根是多少?
的根是多少?
②x取什么值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)直接写出y与x的函数关系式: .
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶.比亚迪油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为![]() 元;若完全用电做动力行驶,则费用为
元;若完全用电做动力行驶,则费用为![]() 元,已知汽车行驶中每千米用油费用比用电费用多
元,已知汽车行驶中每千米用油费用比用电费用多![]() 元.
元.
(1)求:汽车行驶中每千米用电费用是多少元?甲乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过![]() 元,则至少需要用电行驶多少千米?
元,则至少需要用电行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com