
【题目】已知二次函数y=ax2+bx+c的图象抛物线G经过(﹣5,0),(0,![]() ),(1,6)三点,直线l的解析式为y=2x﹣3
),(1,6)三点,直线l的解析式为y=2x﹣3
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
【答案】(1)抛物线G的函数解析式为:y=![]() x2+3x+
x2+3x+![]() ;(2)证明见解析;(3)P(﹣1,0).
;(2)证明见解析;(3)P(﹣1,0).
【解析】试题(1)直接把点(﹣5,0),(0,![]() ),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;
),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;
(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x﹣3组成方程组,再根据一元二次方程根的判别式即可得出结论;
(3)把直线y=2x+m与抛物线G的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.
试题解析:(1)∵次函数y=ax2+bx+c的图象抛物线G经过(﹣5,0),(0,![]() ),(1,6)三点,∴
),(1,6)三点,∴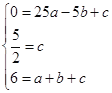 ,解得
,解得![]() ,∴抛物线G的函数解析式为:y=
,∴抛物线G的函数解析式为:y=![]() x2+3x+
x2+3x+![]() ;
;
(2)∵由(1)得抛物线G的函数解析式为:y=![]() x2+3x+
x2+3x+![]() ,∴
,∴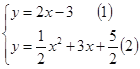 ,
,
①﹣②得,![]() x2+x+
x2+x+![]() =0,∵△=12﹣4×
=0,∵△=12﹣4×![]() ×
×![]() =﹣10<0,∴方程无实数根,即抛物线G与直线L无公共点;
=﹣10<0,∴方程无实数根,即抛物线G与直线L无公共点;
(3)∵与l平行的直线y=2x+m与抛物线G只有一个公共点P,∴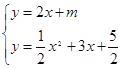 ,消去y得,
,消去y得,![]() x2+x+
x2+x+![]() ﹣m=0①,∵抛物线G与直线y=2x+m只有一个公共点P,∴△=12﹣4×
﹣m=0①,∵抛物线G与直线y=2x+m只有一个公共点P,∴△=12﹣4×![]() ×(
×(![]() ﹣m)=0,解得m=2,把m=2代入方程①得,
﹣m)=0,解得m=2,把m=2代入方程①得,![]() x2+x+
x2+x+![]() ﹣2=0,解得x=﹣1,把x=﹣1代入直线y=2x+2得,y=0,∴P(﹣1,0).
﹣2=0,解得x=﹣1,把x=﹣1代入直线y=2x+2得,y=0,∴P(﹣1,0).


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
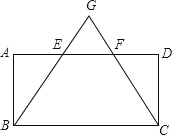
【题目】如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G, GB=GC.
(1)求证:四边形ABCD是矩形;
(2)若△GEF的面积为2.
①求四边形BCFE的面积;
②四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4000元购进一批某品牌的文化衫若干件,很快售完,该店又用6300元钱购进第二批这种文化衫,所进的件数比第一批多40%,每件文化衫的进价比第一批每件文化衫的进价多10元,请解答下列问题:
(1)求购进的第一批文化衫的件数;
(2)为了取信于顾客,在这两批文化衫的销售中,售价保持了一致.若售完这两批文化衫服装店的总利润不少于4100元钱,那么服装店销售该品牌文化衫每件的最低售价是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等边三角形,点P是BC上一动点(点P与点B、C不重合),过点P作PM∥AC交AB于M,PN∥AB交AC于N,连接BN、CM.
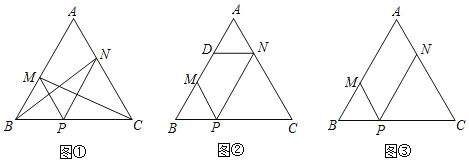
(1)求证:PM+PN=BC;
(2)在点P的位置变化过程中,BN=CM是否成立?试证明你的结论;
(3)如图②,作ND∥BC交AB于D,则图②成轴对称图形,类似地,请你在图③中添加一条或几条线段,使图③成轴对称图形(画出一种情形即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【本小题满分11分】如图,已知抛物线![]() 的顶点D的坐标为(1,
的顶点D的坐标为(1,![]() ),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
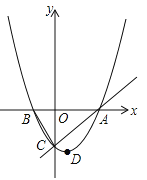
(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标![]() 时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+m)2的顶点坐标为(﹣1,0),且过点A(﹣2,﹣![]() ).
).
(1)求这个二次函数的解析式;
(2)点B(2,﹣2)在这个函数图象上吗?
(3)你能通过左,右平移函数图象,使它过点B吗?若能,请写出平移方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师所留的作业中有这样一个分式的计算题:![]() ,甲、乙两位同学完成的过程分别如下:
,甲、乙两位同学完成的过程分别如下:
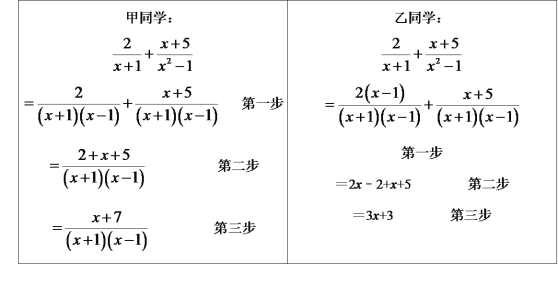
老师发现这两位同学的解答都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
(1)我选择 同学的解答过程进行分析.(填“甲”或“乙”)该同学的解答从第 步开始出现错误,错误的原因是 ;
(2)请重新写出完成此题的正确解答过程.
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com