

分析 解决问题,根据题意证明四边形FD2D1E是平行四边形,根据菱形的判定得到D2F=D2D1,设AD2=xcm,根据菱形的性质列出方程,解方程即可;
拓展延伸,根据平行四边形、矩形、正方形的判定定理解答即可;
拓展迁移,根据题意列出二次函数解析式,求出二次函数的最大值,即可判断.
解答 解:解决问题 可能;平移距离为2.5cm.
∵C1D1∥C2D2,
∴∠C1=∠AFD2.
由题图1的初始位置,得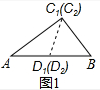
C1D1=C2D2=BD2=AD1=5,
∴∠AC1D1=∠A,
∴在平移到题图2时为∠C1=∠A,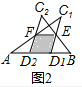
∴∠AFD2=∠A,
∴AD2=D2F.
同理可得BD1=D1E.
∵AD2=BD1,
∴D2F=D1E.
∵D2F∥D1E,
∴四边形FD2D1E是平行四边形.
当D2F=D2D1时,平行四边形FD2D1E才可为菱形.
设AD2=xcm,
∴D2F=xcm,D2D1=(5-x)cm,
∴x=5-x,
∴x=2.5,
∴当平移的距离为2.5cm时,四边形FD2D1E是菱形.
拓展延伸 矩形或正方形.
①∵AD1∥B2C,D1B1∥D2B2,
∴四边形B2FD1E是平行四边形.
∵在△AB1D1中,AB1=10cm,AD1=6cm,B1D1=8cm,
∴△AB1D1是直角三角形,
∴∠AD1B1=90°,
∴当B2E≠B2F时,四边形B2FD1E是矩形.
②由①可知,当B2E=B2F时,四边形B2FD1E是正方形.
拓展迁移 不可能;
理由:设平移距离B2B1为acm,四边形B2FD1E的面积为ycm2.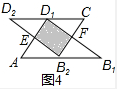
∵B2B1=a,∴AB2=10-a.
由(2)知∠B2FD1=90°,
∴△B1B2F是直角三角形.
∵sinB1=$\frac{3}{5}$,
∴B2F=B2B1•sinB1=$\frac{3}{5}$a,
同理可得B2E=8-$\frac{4}{5}$a,
∴y=B2F•B2E=$\frac{3}{5}$a•(8-$\frac{4}{5}$a)=-$\frac{12}{25}$a2+$\frac{24}{5}$a,
∴y=-$\frac{12}{25}$(a-5)2+12(0<a<10),
∴当a=5时,四边形B2FD1E的面积最大,为12cm2,
∴四边形B2FD1E的面积不可能是13cm2.
点评 本题考查的是平移的性质、菱形的判定和性质以及锐角三角函数的定义的应用和二次函数的性质的应用,掌握平移的性质、二次函数的最值的确定方法、锐角三角函数的概念是解题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
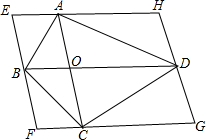 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
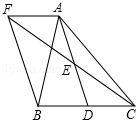 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com