
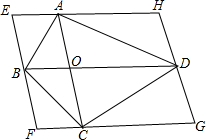
 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.分析 (1)当AC⊥BD时,四边形EFGH是矩形.先证明四边形EFGH是平行四边形,再证明∠EFC=90°即可.
(2)当AC=BD时,四边形EFGH是菱形.只要证明EH=HG即可.
解答 (1)当AC⊥BD时,四边形EFGH是矩形.
证明:∵EF∥AC,HG∥AC,
∴EF∥HG,同理EH∥FG,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴∠AOD=∠EBD=90°,
∵BD∥FG,
∴∠EFG=∠EBD=90°,
∴四边形EFGH是矩形.
(2)当AC=BD时,四边形EFGH是菱形.
证明:由(1)可知四边形EFGH是平行四边形,
∵AC∥HG,AH∥CG,
∴四边形AHGC是平行四边形,
∴AC=GH,
同理四边形EHDB是平行四边形,
∴BD=EH,
∵AC=DB,
∴EH=HG,
∴四边形EFGH是菱形.
点评 本题考查菱形的判定、矩形的判定,熟练掌握这些判定方法是解决问题的关键,记住菱形、矩形的三种判定方法,属于中考常考题型.


科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:填空题
已知关于x的一元二次方程x2+ax+b=0有一个非零根﹣b,则a﹣b的值为_________
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
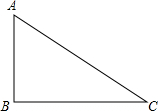 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
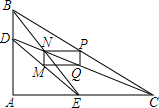 已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.
已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com