
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴相交于点A(-3,0),与y轴交于点B,且与正比例函数y=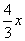 的图象交点为C(m,4)求:
的图象交点为C(m,4)求:
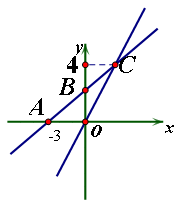
(1)一次函数y=kx+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,直接写出点D的坐标.
(3)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
(1)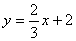 ;
;
(2)(-2,5)或(-5,3).
(3)(5,0)或(-5,0)或(6,0)或(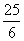 ,0).
,0).
【解析】
分析:(1)首先利用 待定系数法把C(m,4)代入正比例函数y=
待定系数法把C(m,4)代入正比例函数y=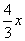 中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式.
中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式.
(2)利用△BED1≌△AOB,△BED2≌△AOB,即可得出点D的坐标.
解:(1)∵点C在正比例函数图像上 ∴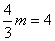 ,
,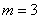
∵点C(3,4)A(—3,0)在一次函数图像上,
∴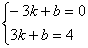
解这个方程组得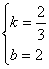
∴一次函数的解析式为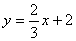
(2)过点D1作D1E⊥y轴于点E,过点D2作D2F⊥x轴于点F,
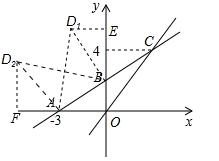
∵点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,∴AB=BD1,
∵∠D1BE+∠ABO=90°,∠ABO+∠BAO=90°,∴∠BAO=∠EBD1,
∵在△BED1和△AOB中,
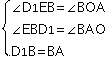
∴△BED1≌△AOB(AAS),
∴BE=AO=3,D1E=BO=2,
即可得出点D的坐标为(-2,5);
同理可得出: △AFD2≌△AOB,
△AFD2≌△AOB,
∴FA=BO=2,D2F=AO=3,
∴点D的坐标为(-5,3).
综上所述:点D的坐标为(-2,5)或(-5,3).
(3)当OC是腰,O是顶角的顶点时,OP=OC=5,则P的坐标是(5,0)或(-5,0);
当OC是腰,C是顶角的顶点时,CP=CO,则P与O关于x=3对称,则P的坐标是(6,0).
当OC是底边时,设P的坐标是(a,0),则
则P的坐标是:(5,0)或(-5,0)或(6,0)或(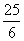 ,0).
,0).
【难度】困难


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
某中学开展“感恩父母”演讲比赛活动,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据下图,分别求出两班复赛的平均成绩和方差;
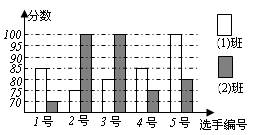
(2)根据(1)的计算结果,哪个班级的复赛成绩较好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列等式:
①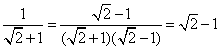 ;
;
②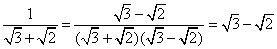 ;
;
③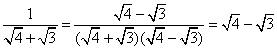 ;
;
……
回答下列问题:
(1)仿照上列等式,写出第n个等式: ;
(2)利用你观察到的规律,化简: ;
;
(3)计算: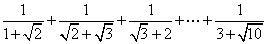 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
设点A的坐标(x,y),其中横坐标x可取-1,2,纵坐标y可取-1,1,2。
(1)求出点A的坐标的所有等可能结果(用树形图或列表法求解);
(2)求点A与点B(1,-1)关于原点对称的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com