
【题目】已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,
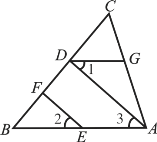
(1)能否得出DG∥BA?试说明理由.(2)EF与BC有什么关系?试说明理由.
【答案】(1)能,DG∥BA,见解析;(2)EF⊥BC,见解析.
【解析】
(1)根据同位角相等,两直线平行,即可得出结论;
(2)先由平行线的性质得到∠1=∠3,又∠1=∠2,所以∠2=∠3,再次推出EF∥AD,即得到∠EFB=∠ADB,已知AD⊥BC于点D,故得到EF与BC的位置关系是垂直.
(1)DG∥BA,
∵∠CDG=∠B(已知),∴DG∥AB(同位角相等,两直线平行),
(2)EF⊥BC
∵∠1=∠3(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠2=∠3,
∴EF∥AD(内同位角相等,两直线平行),
∴∠EFB=∠ADB(两直线平行,同位角相等),
又AD⊥BC于点D(已知),
∴∠ADB=90°,
∴∠EFB=∠ADB=90°,
∴EF⊥CB.


科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
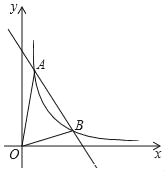
【题目】如图一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(1,6),B(n,2)两点.
(x>0)的图象交于A(1,6),B(n,2)两点.
(1)求一次函数和反比例函数的解析式
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
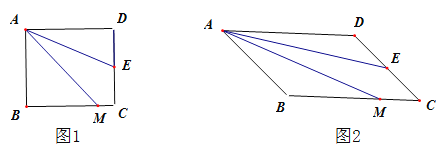
【题目】如图,四边形ABCD是矩形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)证明:AM=AD+MC.
(2)若四边形ABCD是平行四边形,其它条件不变,如图,(1)中的结论是否成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,并探究
①![]()
②![]()
③![]()
……
(1)写出第④个等式:______;
(2)某同学发现,四个连续自然数的积加上1后,结果都将是某一个整数的平方.当这四个数较大时可以进行简便计算,如:
![]() .
.
请你猜想写出第n个等式,用含有n的代数式表示,并通过计算验证你的猜想.
(3)任何实数的平方都是非负数(即![]() ),一个非负数与一个正数的和必定是一个正数(即
),一个非负数与一个正数的和必定是一个正数(即![]() 时,
时,![]() ).根据以上的规律和方法试说明:无论x为什么实数,多项式
).根据以上的规律和方法试说明:无论x为什么实数,多项式![]() 的值永远都是正数.
的值永远都是正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )
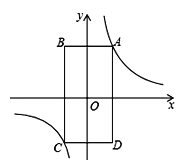
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年入夏以来,由于持续暴雨,某县遭受严重洪涝灾害,群众顿失家园。该县民政局为解决群众困难, 紧急组织了一批救灾帐篷和食品准备送到灾区。已知这批物资中,帐篷和食品共 640 件,且帐篷比食 品多 160 件。
(1)帐篷和食品各有多少件?
(2)现计划租用 A、B 两种货车共 16 辆,一次性将这批物资送到群众手中,已知 A 种货车可装帐蓬40 件和食品 10 件,B 种货车可装帐篷 20 件和食品 20 件,试通过计算帮助民政局设计几种运输 方案?
(3)在(2)条件下,A 种货 车每辆需付运费 800 元,B 种货车每辆需付运费 720 元,民政局应选择 哪种方案,才能使运输费用最少?最少费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com