练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

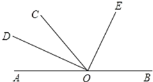
    【题目】如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°．

    （1）求出∠BOD的度数；

    （2）经测量发现：OE平分∠BOC，请通过计算说明道理．

    【答案】（1）；（2）见解析.

    【解析】

    （1）利用角平分线性质求出∠AOD度数，然后利用补角性质进一步计算求解即可；

    (2)根据角平分线性质求出∠DOC=25°，从而得出∠COE，进而根据∠BOC的度数进一步证明即可.

    （1）∵∠AOC=50°，OD平分∠AOC，

    ∴∠AOD=25°，

    ∴∠BOD=180°∠AOD=155°；

    （2）∵∠AOC=50°,

    ∴∠BOC=130°，

    ∵OD平分∠AOC，∠AOC=50°，

    ∴∠DOC=25°，

    ∵∠DOE=90°，

    ∴∠COE=90°25°=65°，

    ∴∠COE=∠BOC，

    ∴OE平分∠BOC.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD的四个顶点分别在反比例函数与(x＞0，0＜m＜n)的图象上，对角线BD//y轴，且BD⊥AC于点P．已知点B的横坐标为4．

    （1）当m=4，n=20时．

    ①若点P的纵坐标为2，求直线AB的函数表达式．

    ②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．

    （2）四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】威远人民商场准备购进甲、乙两种牛奶进行销售，若甲种牛奶的进价比乙种牛奶的进价每件少5元，其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同．

    （1）求甲种牛奶、乙种牛奶的进价分别是多少元？

    （2）若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件，两种牛奶的总数不超过95件，该商场甲种牛奶的销售价格为49元，乙种牛奶的销售价格为每件55元，则购进的甲、乙两种牛奶全部售出后，可使销售的总利润（利润=售价﹣进价）超过371元，请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

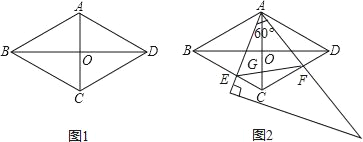
    【题目】如图1，在菱形ABCD中，AC=2，BD=2，AC、BD相交于点O．

    （1）AB的长为　 　；

    （2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF与AC相交于点G．

    ①求证：△ABE≌△ACF；

    ②判断△AEF是哪一种特殊三角形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B在长方形的边上．

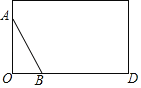
    （1）用圆规和无刻度的直尺在长方形的内部作∠ABC＝∠ABO；（保留作图痕迹，不写作法）

    （2）在（1）的条件下，若BE是∠CBD的角平分线，探索AB与BE的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）

    A. 15 B. 18 C. 21 D. 24

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】试根据图中信息，解答下列问题.

    （1）一次性购买6根跳绳需_____元，一次性购买12根跳绳需______元；

    （2）小红比小明多买2根，付款时小红反而比小明少5元，你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读以下材料并回答问题：

    材料一：已知点 Px0 , y0 和直线 y kx b ，则点Px0 , y0 到直线 y kx b 的距离 d 可以用公式表示为 d . 例如：求点 P 2,1到直线 y x 1的距离.

    解：因为直线 y x 1可以变形为 x y 1 0 ，其中 k 1， b 1，则点 P 2,1到直线y x 1的距离可以表示为 d =.

    材料二：对于直线 y1 k1 x b1 与直线 y2 k2 x b2 ，若 y1 // y2 ，那么 k1 k2 且b1 b2 ，若 y1 y2 ，那么 k1 k2 1.

    （1）点 P1,1到直线 y 2x 1的距离为 ；

    （2）已知直线 y1 x 与直线y2 k2 x 1平行，且在平面内存在点到直线 y2 k2 x 1的距离是其到直线 y1 x 距离的两倍，求点所在直线的解析式；

    （3）已知直线与直线垂直，其交点为Q，在平面内存在点P(点P不在直线与直线上),过点P分别向直线与直作垂线，垂足分别为M、N，若MQNP是边长为的正方形，求点P点坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学八年级举行跳绳比赛，要求每班选出5名学生参加，在规定时间每人跳绳不低于150次为优秀，冠、亚军在八（1）、八（5）两班中产生．下表是这两个班的5名学生的比赛数据（单位：次）

    1号

    2号

    3号

    4号

    5号

    平均数

    方差

    八（1）班

    139

    148

    150

    160

    153

    150

    46.8

    八（5）班

    150

    139

    145

    147

    169

    150

    103.2

    根据以上信息，解答下列问题：

    （1）求两班的优秀率及两班数据的中位数；

    （2）请你从优秀率、中位数和方差三方面进行简要分析，确定获冠军奖的班级．

    查看答案和解析>>

    同步练习册答案