
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③S△FGC=![]() .其中正确的是( )
.其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
【答案】B
【解析】分析:先求出DE、CE的长,再根据翻折的性质可得AD=AF,EF=DE,∠AFE=∠D=90°,再利用“HL”证明Rt△ABG和Rt△AFG全等,根据全等三角形对应边相等可得BG=FG,再设BG=FG=x,然后表示出EG、CG,在Rt△CEG中,利用勾股定理列出方程求出x=![]() ,从而可以判断①正确;根据∠AGB的正切值判断∠AGB≠60°,从而求出∠CGF≠60°,△CGF不是等边三角形,FG≠FC,判断②错误;先求出△CGE的面积,再求出EF:FG,然后根据等高的三角形的面积的比等于底边长的比求解即可得到△FGC的面积,判断③正确.
,从而可以判断①正确;根据∠AGB的正切值判断∠AGB≠60°,从而求出∠CGF≠60°,△CGF不是等边三角形,FG≠FC,判断②错误;先求出△CGE的面积,再求出EF:FG,然后根据等高的三角形的面积的比等于底边长的比求解即可得到△FGC的面积,判断③正确.
详解:∵正方形ABCD中,AB=3,CD=3DE,
∴DE=![]() ×3=1,CE=3-1=2,
×3=1,CE=3-1=2,
∵△ADE沿AE对折至△AFE,
∴AD=AF,EF=DE=1,∠AFE=∠D=90°,
∴AB=AF=AD,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
设BG=FG=x,则EG=EF+FG=1+x,CG=3-x,
在Rt△CEG中,EG2=CG2+CE2,
即(1+x)2=(3-x)2+22,
解得,x=![]() ,
,
∴CG=3-![]() =
=![]() ,
,
∴BG=CG=![]() ,
,
即点G是BC中点,故①正确;
∵tan∠AGB= ![]() =2,
=2,
∴∠AGB≠60°,
∴∠CGF≠180°-60°×2≠60°,
又∵BG=CG=FG,
∴△CGF不是等边三角形,
∴FG≠FC,故②错误;
△CGE的面积=![]() CGCE=
CGCE=![]() ×
×![]() ×2=
×2=![]() ,
,
∵EF:FG=1:![]() =2:3,
=2:3,
∴S△FGC=![]() ,故③正确;
,故③正确;
综上所述,正确的结论有①③.
故选B.


科目:初中数学 来源: 题型:
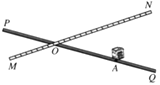
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为()
A. ![]() 秒 B. 16秒 C.
秒 B. 16秒 C. ![]() 秒 D. 24秒
秒 D. 24秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE= ![]()

(1)求证:BC是⊙O的切线;
(2)求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是 , cosA的值是 . (结果保留根号) 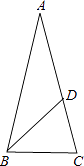
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.

(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城市群的建设与发展,在A,B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的120km缩短至114km,城际铁路的设计平均时速要比现行的平均时速快110km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A,B两地的运行时间.
,求建成后的城际铁路在A,B两地的运行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1 , a2 , …,a2017是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2017=84,(a1+1)2+(a2+1)2+…+(a2017+1)2=4001,则a1 , a2 , …,a2017中为0的个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com