
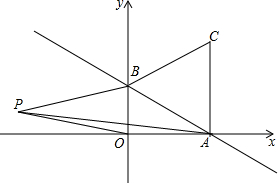
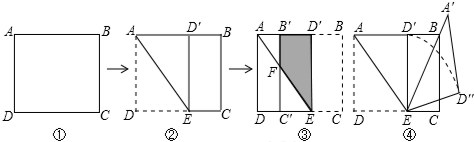
 ��ͼ��һ�κ���y=-$\frac{\sqrt{3}}{3}$x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ���������ȱߡ�ABC��
��ͼ��һ�κ���y=-$\frac{\sqrt{3}}{3}$x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ���������ȱߡ�ABC������ ��1������һ�κ���y=-$\frac{\sqrt{3}}{3}$x+1���A��B��������꣬��������֮��ľ��빫ʽ���AB�ij�����C��CD��AB��D�����ݵȱ������ε����ʼ�����ǵ����Ǻ���ֵ�����CD�ij������������ε������ʽ��⼴�ɣ�
��2��������֪�����������ε������ʽ�ó�S��AOB��S��AOP��S��BOP��������ٸ���S��ABP=S�ı���ABPO-S��APO�͡�ABP��������ABC�������ȣ��������a��ֵ��
��3�����ݵ�A�������AB��ֵ���ֱ���ABΪ���͵�ʱ���������������M�����꼴�ɣ�
��� 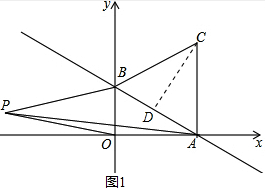 �⣺��1����ͼ1������C��CD��AB��
�⣺��1����ͼ1������C��CD��AB��
��x=0��y=1����y=0����x=$\sqrt{3}$����A��$\sqrt{3}$��0����B��0��1����
AB=$\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2��
��C��CD��AB��D��
�ߡ�ABC�ǵȱ������Σ���BD=$\frac{1}{2}$AB=$\frac{1}{2}$��2=1��
��CD=BD•tan60��=1��$\sqrt{3}$=$\sqrt{3}$��
��S��ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$��2��$\sqrt{3}$=$\sqrt{3}$��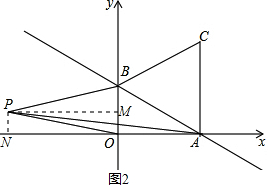 ��2����ͼ2������P��PM��y�ᣬPN��x�ᣬ��y����һ��M��x����һ��N��
��2����ͼ2������P��PM��y�ᣬPN��x�ᣬ��y����һ��M��x����һ��N��
��A��$\sqrt{3}$��0����B��0��1����P��a��$\frac{1}{2}$����
��S��AOB=$\frac{1}{2}$��$\sqrt{3}$��1=$\frac{\sqrt{3}}{2}$��S��AOP=$\frac{1}{2}$��$\sqrt{3}$��$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$��S��BOP=$\frac{1}{2}$|a|•OB=-$\frac{a}{2}$��
��S�ı���ABPO=S��AOB+S��BOP=$\frac{\sqrt{3}-a}{2}$
��S��ABP=S�ı���ABPO-S��APO��
�൱��ABP��������ABC��������ʱ��$\frac{\sqrt{3}-a}{2}$-$\frac{\sqrt{3}}{4}$=$\sqrt{3}$��
��ã�a=-$\frac{3}{2}$$\sqrt{3}$��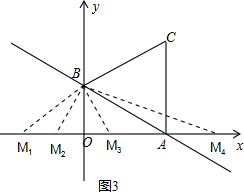
��3����ͼ3���ߡ�MABΪ���������Σ�A��$\sqrt{3}$��0����
��M1��-$\sqrt{3}$��0����
��AB=$\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2��
��AM2=2��
��M2��$\sqrt{3}$-2��0����
ͬ���ɵã�M3��$\frac{\sqrt{3}}{3}$��0����M4��$\sqrt{3}$+2��O����
�����������ĵ�M��4����M1��-$\sqrt{3}$��0����M2��$\sqrt{3}$-2��0����M3��$\frac{\sqrt{3}}{3}$��0����M4��$\sqrt{3}$+2��O����
���� ���⿼����һ�κ������ۺϣ��õ���֪ʶ���ǹ��ɶ����������ε������ʽ�Լ����������ε����ʣ��ؼ��Ǹ������⻭��ͼ�Σ�ע�ⲻҪ©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
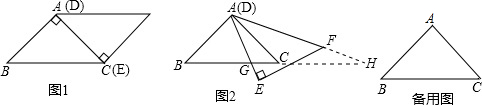
 Ϊ��̽������ʽ$\sqrt{{x^2}+4}+\sqrt{{{��{9-x}��}^2}+1}$����Сֵ��С������������ˡ����ν�ϡ�˼�룮���巽���������ģ���ͼ��CΪ�߶�BD��һ���㣬�ֱ����B��D��AB��BD��ED��BD������AC��EC����֪AB=2��DE=1��BD=9����BC=x����$AC=\sqrt{{x^2}+4}$��$CE=\sqrt{{{��{9-x}��}^2}+1}$�������⼴ת������AC+CE����Сֵ��
Ϊ��̽������ʽ$\sqrt{{x^2}+4}+\sqrt{{{��{9-x}��}^2}+1}$����Сֵ��С������������ˡ����ν�ϡ�˼�룮���巽���������ģ���ͼ��CΪ�߶�BD��һ���㣬�ֱ����B��D��AB��BD��ED��BD������AC��EC����֪AB=2��DE=1��BD=9����BC=x����$AC=\sqrt{{x^2}+4}$��$CE=\sqrt{{{��{9-x}��}^2}+1}$�������⼴ת������AC+CE����Сֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ÿ��ˮ���� | ���� |
| ������6m3���� | 2Ԫ/m3 |
| ����6m3������10m3�IJ��� | 4Ԫ/m3 |
| ����10m3�IJ��� | 8Ԫ/m3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������ | �����ҵ� | |
| A | ||
| B |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com