
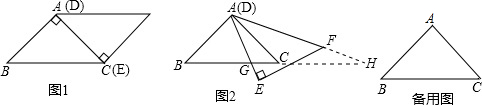
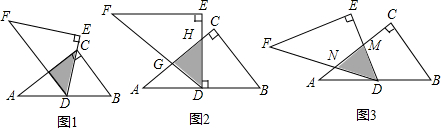
分析 (1)由等腰直角三角形的性质与三角形外角的性质,易得∠GAC=∠H,然后由公共角相等,即可得△AGC∽△HGA;由∠B=∠ACG=45°,即可得△AGC∽△HAB;
(2)此题要采用分类讨论的思想,当CG<$\frac{1}{2}$BC时,当CG=$\frac{1}{2}$BC时,当CG>$\frac{1}{2}$BC时分别得出即可;
(3)作AP⊥BC,运用三角函数和勾股定理求出CG,然后根据相似三角形的对应边的比相等,列出BH和CG的关系式;
解答 解:(1)有△HGA和△HAB,
理由是:如图1,∵△ABC中,∠BAC=90°,AB=AC,
△DEF中,∠DEF=90°,DE=EF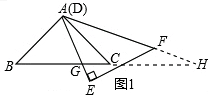
∴∠B=∠ACB=∠EDF=45°,
∴∠H+∠CAH=∠ACB=45°,∠GAC+∠CAH=∠EDF=45°,
∴∠H=∠GAC,∠EDF=∠ACB=∠B=45°,
∴△始终与△AGC相似的三角形有△HGA和△HAB,
故答案为:△HGA和△HAB;
(2)①当CG<$\frac{1}{2}$BC时,∠GAC=∠H<∠HAC,
∴AC<CH,
∵AG<AC,
∴AG<CH<GH,
又∵AH>AG,AH>GH,
此时,△AGH不可能是等腰三角形,
②当CG=$\frac{1}{2}$BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,
此时,GC=$\frac{9\sqrt{2}}{2}$,即x=$\frac{9\sqrt{2}}{2}$,
③当CG>$\frac{1}{2}$BC时,由(1)△AGC∽△HGA,
∴,若△AGH必是等腰三角形,只可能存在GH=AH,若GH=AH,则AC=CG,此时x=9,
如图2,当CG=BC时,
注意:DF才旋转到与BC垂直的位置,
此时B,E,G重合,∠AGH=∠GAH=45°,
∴△AGH为等腰三角形,所以CG=9$\sqrt{2}$.
综上所述,当x=9或x=$\frac{9\sqrt{2}}{2}$或9$\sqrt{2}$时,△AGH是等腰三角形.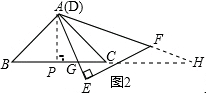
(3)$\frac{{27\sqrt{2}+9\sqrt{6}}}{2}$
如图2,作AP⊥BC,
∵△ABC是等腰直角三角形,AB=9,
∴AP=PC=$\frac{9\sqrt{2}}{2}$,
又∵∠GAC=15°,∠ACB=45°,
∴∠AGP=60°,
∴PG=$\frac{AP}{tan60°}$=$\frac{\frac{9\sqrt{2}}{2}}{\sqrt{3}}=\frac{3\sqrt{6}}{2}$,
∴CG=PC-PG=$\frac{9\sqrt{2}}{2}$-$\frac{3\sqrt{6}}{2}$,
∵△AGC∽△HAB,
∴$\frac{CG}{AB}=\frac{AC}{BH}$
∴$\frac{\frac{9\sqrt{2}}{2}-\frac{3\sqrt{6}}{2}}{9}=\frac{9}{BH}$,
解得:BH=$\frac{27\sqrt{2}+9\sqrt{6}}{2}$.
故答案为:$\frac{27\sqrt{2}+9\sqrt{6}}{2}$.
点评 此题主要考查学生对相似三角形的判定与性质,等腰三角形的性质,等腰直角三角形的性质,旋转的性质等知识点的理解和掌握,综合性较强,难易程度适中,是一道很典型的题目.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
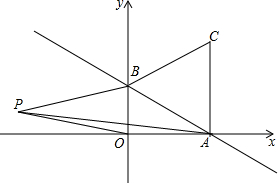 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com