
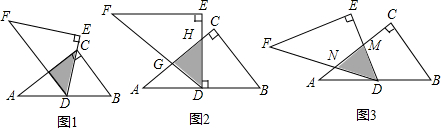
分析 (1)确定点G为AC的中点,从而△ADC为等腰三角形,其底边AC=8,底边上的高GD=$\frac{1}{2}$BC=3,从而面积可求;
(2)本问解法有多种,解答中提供了三种不同的解法.基本思路是利用相似三角形、勾股定理求解;
(3)对于爱心小组提出的问题,如答图4所示,作辅助线,利用相似三角形、勾股定理、等腰三角形的性质,列方程求解.
解答 解:(1)【独立思考】
∵∠ACB=90°,D是AB的中点,
∴DC=DA=DB,
∴∠B=∠DCB.
又∵△ABC≌△FDE,
∴∠FDE=∠B.
∴∠FDE=∠DCB,
∴DG∥BC.
∴∠AGD=∠ACB=90°,
∴DG⊥AC.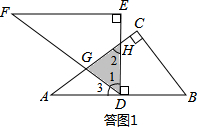
又∵DC=DA,
∴G是AC的中点,
∴CG=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4,DG=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∴S△DGC=$\frac{1}{2}$CG•DG=$\frac{1}{2}$×4×3=6.
(2)【合作交流】如下图所示:
∵△ABC≌△FDE,
∴∠B=∠1.
∵∠C=90°,ED⊥AB,
∴∠A+∠B=90°,∠A+∠2=90°,
∴∠B=∠2,
∴∠1=∠2,
∴GH=GD.
∵∠A+∠2=90°,∠1+∠3=90°,
∴∠A=∠3,
∴AG=GD,
∴AG=GH,即点G为AH的中点.
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2+}{6}^{2}}$=10,
∵D是AB中点,
∴AD=$\frac{1}{2}$AB=5.
在△ADH与△ACB中,
∵∠A=∠A,∠ADH=∠ACB=90°,
∴△ADH∽△ACB,
∴$\frac{AD}{CD}=\frac{DH}{CB}$,即$\frac{5}{8}=\frac{DH}{6}$,解得DH=$\frac{15}{4}$,
∴S△DGH=$\frac{1}{2}$S△ADH=$\frac{1}{2}$×$\frac{1}{2}$×DH•AD=$\frac{1}{4}$×$\frac{15}{4}$×5=$\frac{75}{16}$.
(3)【提出问题】解决“爱心”小组提出的问题.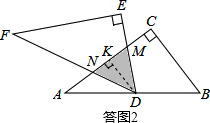
如答图4,过点D作DK⊥AC于点K,则DK∥BC,
又∵点D为AB中点,
∴DK=$\frac{1}{2}$BC=3.
∵DM=MN,
∴∠MND=∠MDN,由(2)可知∠MDN=∠B,
∴∠MND=∠B,
又∵∠DKN=∠C=90°,
∴△DKN∽△ACB,
∴$\frac{KN}{BC}=\frac{DK}{AC}$,即$\frac{KN}{6}=\frac{3}{8}$,得KN=$\frac{9}{4}$.
设DM=MN=x,则MK=x-$\frac{9}{4}$.
在Rt△DMK中,由勾股定理得:MK2+DK2=MD2,
即:(x-$\frac{9}{4}$)2+32=x2,解得x=$\frac{25}{8}$,
∴S△DMN=$\frac{1}{2}$MN•DK=$\frac{1}{2}$×$\frac{25}{8}$×3═$\frac{75}{16}$.
点评 本题是几何综合题,考查了相似三角形、全等三角形、等腰三角形、勾股定理、图形面积计算、解方程等知识点.题干信息量大,篇幅较长,需要认真读题,弄清题意与作答要求.试题以图形旋转为背景,在旋转过程中,重叠图形的形状与面积不断发生变化,需要灵活运用多种知识予以解决,有利于培养同学们的研究与探索精神,激发学习数学的兴趣,是一道好题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a+b | B. | a+b+3 | C. | 3(a+b) | D. | $\frac{1}{3}$a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每月水用量 | 单价 |
| 不超出6m3额额部分 | 2元/m3 |
| 超出6m3不超出10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
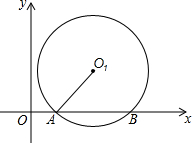 如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.
如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com