
| A. | 3a+b | B. | a+b+3 | C. | 3(a+b) | D. | $\frac{1}{3}$a+b |
分析 根据数据m1、m2、m3的平均数为a,可得m1+m2+m3=3a,进一步得到3m1+3m2+3m3=9a,根据数据n1、n2、n3的平均数为b,可得n1+n2+n3=3b,依此即可得到数据3m1+n1、3m2+n2、3m3+n3的和,再根据平均数公式即可求解.
解答 解:∵数据m1、m2、m3的平均数为a,
∴m1+m2+m3=3a,
∴3m1+3m2+3m3=9a,
∵数据n1、n2、n3的平均数为b,
∴n1+n2+n3=3b,
∴数据3m1+n1+3m2+n2+3m3+n3=9a+3b,
∴数据3m1+n1、3m2+n2、3m3+n3的平均数是(9a+3b)÷3=3a+b.
故选:A.
点评 本题考查的是样本平均数的求法及运用,即平均数公式:$\overline{x}$=$\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题
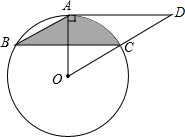 如图,⊙O经过?ABCD的三个顶点A,B,C,且圆心O在DC的延长线上,∠D=30°,AD=6$\sqrt{3}$cm.
如图,⊙O经过?ABCD的三个顶点A,B,C,且圆心O在DC的延长线上,∠D=30°,AD=6$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是由24个小方格组成的轴对称图形,请你用剪刀剪三下,把它分成四块形状大小完全相同的图案,并使分出的小图案也是轴对称图形,你知道怎样剪吗?
如图,是由24个小方格组成的轴对称图形,请你用剪刀剪三下,把它分成四块形状大小完全相同的图案,并使分出的小图案也是轴对称图形,你知道怎样剪吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
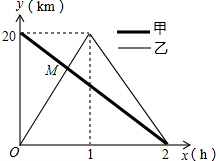 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com