

分析 (1)设爸爸的速度为x m/min,则小明的速度为$\frac{3}{4}x$m/min,根据爸爸的话列出方程并解答;
(2)分两种情况:小明在爸爸的前方和后方,根据时间=路程差÷速度差列出算式求解即可.
解答 解:(1)设爸爸的速度为xm/min,则小明的速度为$\frac{3}{4}x$m/min,
根据题意得:$4(x-\frac{3}{4}x)=400$,
解得:x=400,
$\frac{3}{4}x$=$400×\frac{3}{4}=300$.
答:小明的速度为300m/min,爸爸的速度为400m/mim;
(2)50÷(400-300)
=50÷100
=0.5(分钟);
(400-50)÷(400-300)
=350÷100
=3.5(分钟)‘
答:再经过0.5或3.5分钟,小明和爸爸在跑道上相距50m.
故答案为:0.5或3.5.
点评 考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,由路程差找出合适的等量关系列出方程,再求解.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
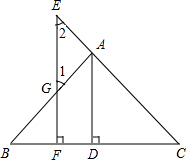 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
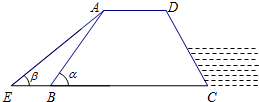 如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的坡长为AE,背水面坡角β=45°.若原坡长AB=16m,求改造后的坡长AE(结果保留根号).
如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的坡长为AE,背水面坡角β=45°.若原坡长AB=16m,求改造后的坡长AE(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
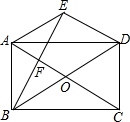 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com